概率论(4)
一道压轴题引发的思考~
题目分析
题目如下:
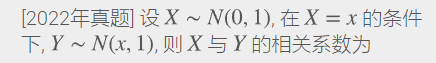
这个题目就这么短,而且也非常的清晰,却是 22 年的选择压轴题,这题深入做过之后发现常规的很多做法都需要记住一些公式或者是较大的计算量(答案确实也如此)。
而在这里我感觉到可以使用另外一种比较简单的思路做出这题。
解题
首先从题目描述提取信息之后得到以下两个比较重要的信息。
$X \sim N(0,1),f_X(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$
$Y|X\sim N(x,1),f_{Y|X}(y,x)=\frac{1}{\sqrt{2\pi}}
e^{-\frac{(y-x)^2}{2}}$
这里直接利用条件概率的公式就能得到 X 和 Y 的二维概率密度的函数。当然二维概率密度的公式我们肯定是不会去背下来的,而且考试的时候真不要指望自己记得。
得到
$f_{X,Y}(x,y)=\frac{1}{2\pi}e^{-\frac{x^2+(y-x)^2}{2}}$
这里我们其实很容易就看出来了,这相当于是两个都服从 $N(0,1)$ 的随机变量的乘积并且它们都独立。
我们知道,二维随机变量的概率密度函数如果满足 $f_X(x)\times f_Y(y)=f_{X,Y}(x,y)$ 的话,它们一定是独立的。
那么上面我们可以令 $Z=Y-X$,那么 $Z\sim N(0,1)$,且和 $X$ 是独立的。
$Y=Z+X$,因为这里 $Z$ 和 $X$ 是独立的,所以它们相加之后,$Y\sim N(0,2)$。
$E(XY)=E(X(Z+X))=E(X^2)+E(ZX)$
这个式子当中,$E(X^2)$ 我们可以直接 $E(X^2)=D(X)+E(X)^2$ 得到,而我们都知道 $X$ 服从什么分布了,它的期望方差当然也不难得到,所以 $E(X^2)=1$,后面那个部分,由于 $Z$ 和 $X$ 是独立的,所以 $E(ZX)=E(X)E(Z)=0$。
当然 $E(X)=E(Y)=0$ 也是显而易见的。
最后我们根据相关系数的公式 $\rho_{x,y}=\frac{E(XY)-E(X)E(Y)}{\sqrt{D(X)D(Y)}}$
这里最主要的 $E(X)$ 都算出来了,剩下的基本都是题目有的,所以最后答案应该就是 $\frac{\sqrt{2}}{2}。$
我是没想过这题可以这么解的,而且我已知的答案貌似都没有这种的解法,但是我恰恰认为这种解法才比较像考试可以想到的做法。