概率论(3)
参数估计和置信区间计算。
引入
很多老师都用这样的一个例子引入,假设我想知道全国身高的均值。这个值 $\mu$ 必然是客观存在的,但是给全国十四亿人全部测一遍显然这个工作量太大,对于学过数理统计的人来说,解决这个的最好的办法自然就是抽样。
理论
极限中心定理告诉我们,当样本量足够大时,所有的分布最终都趋于正态分布,下图就是标准正态分布的概率密度图。
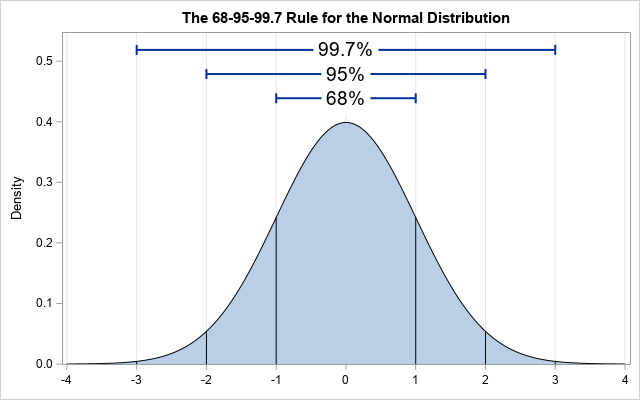
概率密度函数反映了概率在该点的变化率,变化率越大显然证明该点的概率越大(即样本值等于该值的概率越大)。
因此正态分布的特点就是:均值的概率最大,越远离平均值的数值被抽到的概率越小。
而我们是想通过抽象来获得总体的平均值,而样本平均值显然是不能等于平均值的,但是可以一定程度地反应,那么如何描述这个“一定程度”,就是使用显著性水平来描述。
例如,从图中我们可以看出,-2~2 区间内的值包含了 95% 的概率,也就是说绝对值 > 2 的可能性仅仅只有 5%,这个 5% 就是显著性水平 $\alpha$,对应的置信水平就是 $1-\alpha$,而如果能找到一个区间,使得该区间的概率刚好等于置信水平的最小区间称为置信区间。
举个例子就是:假如投100个骰子,请你找出一个最小区间,使得这100个投掷出的点的和有95%的概率落入区该间内,那么我们所找到的这个最小区间就是显著性水平为 5% 的置信区间。
当然人的身高均值不可能是等于 0 的,它会服从 $N(\mu,\sigma^2)$ 的正态分布。假设 $\mu$ 未知,$\sigma$ 已知,我们是能画出它的概率密度图的, $\mu$ 的影响仅仅只是在 X 轴上平移罢了。
我们抽样之后,可以算出来一个样本的均值 $\overline X$,显然,这个均值应当服从 $N(\mu,\frac{\sigma^2}{n})$,$n$ 为抽样数量。
对这个随机变量进行正态标准化之后(这里我们会假定总体均值 $\mu=\hat{\mu}$),得到 $\frac{\overline X-\hat\mu}{\frac{\sigma}{\sqrt{n}}}$,它的值应当也有 95% 的概率落入 -2~2,如果恰好没有落入 -2~2,当然小概率事件是有可能发生的,但是一旦一次抽样发生了小概率事件,我们认为这件事就不对,也就是 $\overline X$ 不服从均值为 $\hat\mu$ 的分布,即我们没有 95% 的把握认为 $\mu=\hat\mu$。
分位点
其实很简单,概率论里面的分位点有两个,一个是(普通)分位点,一个是上分位点。
对于一个概率密度图来说:
如果存在一个值 $X$ 使得 $P{X\ge\alpha}$,那么该值就叫该概率密度函数的上 $\alpha$ 分位点,记为 $f_\alpha$。
如果存在一个值 $X$ 使得 $P{X\le\alpha}$,那么该值就叫该概率密度函数的 $\alpha$ 分位点,记为 $f_{1-\alpha}$。
计算置信区间
显然,在我们把均值变量标准化之后,我们需要找到对应的置信区间,来看看它在不在置信区间内。即:$\frac{\overline X-\hat\mu}{\frac{\sigma}{\sqrt{n}}}\in [\phi_{1-\frac{\alpha}{2}},\phi_{\frac{\alpha}{2}}]$,通过分位点,我们很容易找到置信区间,而即使我们不把它标准化,我们也可以利用化简不等式的方式轻易找到均值的置信区间,简单讲就是我们可以找到一个身高的范围,让它的抽样结果大概率是在里面的。
假设我们抽样100次,总体标准差为 5cm,假如我要认为全国人民的平均身高是 160cm,那么应当有$\frac{\overline X-160}{\frac{5}{\sqrt{100}}}\in [-2,2]$,即可化简出 $\overline X\in [159,161]$,如果抽样结果在里面,我们有 95%的概率相信全国人民的平均身高就是 160cm,如果不是,那么我们认为全国人民的平均身高就不是 160cm,如果没有明确告诉我们显著性水平,只给了我们一个 $\alpha$ 代替,我们可以使用分位点来代替这里的数值,即 $\overline X \in [160+\frac{1}{2}\phi_{1-\frac{\alpha}{2}},160+\phi_{\frac{\alpha}{2}}]$,如果 n 和和我们所预估的均值也是符号呢,那就一样的往回带就好了 $\overline X \in [\hat\mu+\frac{\sigma}{\sqrt{n}}\phi_{1-\frac{\alpha}{2}},\hat\mu+\frac{\sigma}{\sqrt{n}}\phi_{\frac{\alpha}{2}}]$,所以我们很容易得到已知方差情况下的置信区间。
这里需要注意的一点是,我们是在已知方差的情况下计算的,但是实际情况是,我连均值都不知道何来的方差?这个时候就需要用样本方差来代替总体方差,而这里也不再服从正态分布,而是服从学生分布(也叫t分布)。根据 t 分布的定义,我们很容易得出,它和正态分布的图像是差不多的,我们也仅仅只需要把上面式子中的 $\sigma$ 用样本标准差 S 代替就得到了学生分布,而这里样本容量决定了 t 分布的自由度。
这里简单推一即可:
根据定义我们知道 $\frac{\overline X-\hat\mu}{\frac{S}{\sqrt{n}}}\sim t(n-1)$,同样利用分位点的定义,我们可以计算得出,样本容量为 n ,样本标准差为 S,估计均值为 $\hat\mu$ 的置信区间就是 $\overline X \in [\hat\mu+\frac{S}{\sqrt{n}}t_{1-\frac{\alpha}{2}}(n-1),\hat\mu+\frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}(n-1)]$。
样本方差置信区间计算
同样根据定义我们有 $\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1)$,根据分位点,我们可以得到 $\frac{(n-1)S^2}{\sigma^2} \in [\chi^2_{1-\frac{\alpha}{2}}(n-1),\chi^2_{\frac{\alpha}{2}}(n-1)]$,后面应该挺简单的,就是不等式化简,得到 $\sigma^2\in[\frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}}(n-1)},\frac{(n-1)S^2}{\chi^2_{1-\frac{\alpha}{2}}(n-1)}]$。
两个正态分布方差比值的置信区间计算
这里我们假设两个正态分布的方差分别为 $\sigma_1^2,\sigma_2^2$,我们从第一个正态分布抽取了 $n_1$ 个样本,标准差为 $S_1$,第二个正态分布抽取了 $n_2$ 个样本,标准差为 $S_2$。从上面过来,我们知道两个卡方分布比它们各自的自由度的比值应该是服从 F 分布的,F分布的自由度分别为两个卡方分布的自由度。
$\frac{\frac{(n_1-1)S_1^2}{\sigma_1^2}}{\frac{(n_2-1)S_2^2}{\sigma_2^2}}\sim \frac{\chi^2(n_1-1)}{\chi^2(n_2-1)}$,像上面说的,每个卡方分布除它们的自由度,得到了F分布,因此 $\frac{\frac{S_1^2}{\sigma_1^2}}{\frac{S_2^2}{\sigma_2^2}}\sim F(n_1-1,n_2-1)$,再整理一下就是 $\frac{S_1^2\sigma_2^2}{S_2^2\sigma_1^2}\sim F(n_1-1,n_2-1)$,再根据分位点计算出这个随机变量的置信区间:$\frac{S_1^2\sigma_2^2}{S_2^2\sigma_1^2}\in[F_{1-\frac{\alpha}{2}}(n_1-1,n_2-1),F_{\frac{\alpha}{2}}(n_1-1,n_2-1)]$
这里化简比较简单了,没有加加减减,直接乘过去那个标准差的比值就行了,$\frac{\sigma_2^2}{\sigma_1^2}\in[\frac{S_1^2}{S_2^2}F_{1-\frac{\alpha}{2}}(n_1-1,n_2-1),\frac{S_1^2}{S_2^2}F_{\frac{\alpha}{2}}(n_1-1,n_2-1)]$,这里需要最后一个 F 分布的公式,那就是交换 F 分布的自由度之后,原分位点会变成上分位点的倒数。即:$F_{1-\frac{\alpha}{2}}(n_1-1,n_2-1)=\frac{1}{F_{\frac{\alpha}{2}}(n_2-1,n_1-1)}$,这个结论记住就行了,也不难,因此上面的置信区间也不唯一,可以根据给定的条件灵活变换。
以上所有置信区间的公式我觉得并不需要会背,但是要会推,根据一个变量服从什么样的分布,通过分位点计算区间,然后再倒回去推出你所需要的随机变量的置信区间。