和sigma姐姐vp这场icpc。
D. Journey to Un’Goro 这题是构造题,本来有思路了的,但是没敢提交。
题目描述 题目解析 就是说给定一个长度,你需要构造一个只有 r 和 b 字符的字符串,在字符串的子串中,如果有奇数个r,这就是个好区间。问你一个这样长度的字符串最多有多少个好区间,并构造出最好的情况,按字典序输出,如果超过100个则输出前100个。
我们思考一下如何去计算最大值,就得先看看怎么去计数,首先暴力计数需要 $n^2$ 就肯定不行。因为是奇数个,所以我们考虑转化成前缀和。那么我们看看,如果只有一个 r 其它全是 b 我们看哪些区间符合条件。这里我们不妨把 r 当成 1,把 b 当成 0。
1 2 b b b b r r r b b b 0 0 0 0 1 2 3 3 3 3
可以很容易发现,当前缀和相减之后为奇数时,区间是好区间。那么就是偶数匹配奇数其实,因为偶数减奇数或者奇数减偶数才有可能得到奇数,而前缀和要么是偶数要么是奇数。我们最终得到的结果就是 $num=cnt_{odd}\times cnt_{even}$ 而我们很容易得到 $cnt_{odd}+cnt_{even}=n$ ,根据基本不等式我们不难得到当 $cnt_{odd}$ 与 $cnt_{even}$ 接近的时候 $num$ 得到最大值。
因为 $n$ 可能是奇数,所以我这里说的是接近。那么奇数就是一个多一个一个少一个,偶数就是都一样就好了。
那么这个可以直接算出来的。
$ans=\frac{n}{2}\times \frac{n+1}{2}$
那么主要就是怎么构造了,也很简单,既然要字典序,我们就尽量构造 b 实在不行就构造 r。什么叫实在不行呢?那就是前缀和奇数个数超过了 (n+1)/2 这个时候就肯定不行。
标程 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <bits/stdc++.h> using namespace std;#define int long long #define rep(i, x, y) for(int i=(x);i<=(y);++i) #define dep(i, x, y) for(int i=(x);i>=(y);--i) #define gcd(a, b) __gcd(a,b) const long long mod = 1e9 + 7 ;const int maxn = 1e6 + 10 ;int a[maxn]; int n;char s[maxn];int cnt=0 ;int flag=0 ;int p[maxn];int dfs (int pos,int n1,int n2) if (n1>cnt||n2 > cnt) return 0 ; if (flag==100 )return 1 ; if (pos==n+1 ){ flag++; for (int i=1 ;i<=n;i++)cout<<s[i]; cout<<endl; return 0 ; } int res=0 ; s[pos]='b' ; p[pos]=p[pos-1 ]; p[pos] == 1 ? res=dfs (pos + 1 , n1 + 1 , n2) : res=dfs (pos + 1 , n1, n2 + 1 ); if (res==1 )return 1 ; s[pos]='r' ; p[pos-1 ]==1 ?p[pos]=2 :p[pos]=1 ; p[pos] == 1 ? res = dfs (pos + 1 , n1 + 1 , n2) : res = dfs (pos + 1 , n1, n2 + 1 ); if (res)return 1 ; } signed main () p[0 ]=2 ; cin>>n; int z=ceil ((double )(n+1 )/2 ); cout<<z*((n+1 )/2 )<<endl; cnt= z; dfs (1 ,0 ,1 ); return 0 ; }
F. Kobolds and Catacombs 题目描述 题目分析 就是要把一个序列划分,要尽可能地多划分,被划分的序列在一个内部进行排序,最后要求整个序列不递减。那么我们一开始是很容易想到如果元素 $p_i$ 原本需要在 $j$ 的位置上,那么 $i-j$ 的位置上都应该被划分为一个集合。虽然想到了这点,但是其实还可以用这样一种方式做:前缀和!和排过序的前缀和做比较,当有一个位置前缀和相同则 +1,最后输出答案即可,这个思维一定要想到,是sigma姐姐想出来的,我根本没想到qwq。
标程 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <bits/stdc++.h> #define maxn 1000005 #define int long long using namespace std;struct A { int value; int index; }a[maxn]; int vis[maxn];int cmp (A a,A b) return a.value<b.value; } int sum1[maxn],sum2[maxn]; void solve () int n; scanf ("%lld" ,&n); for (int i=1 ;i<=n;i++){ scanf ("%lld" ,&a[i].value); a[i].index=i; } for (int i=1 ;i<=n;i++){ sum1[i]=sum1[i-1 ]+a[i].value; } sort (a+1 ,a+1 +n,cmp); for (int i=1 ;i<=n;i++){ sum2[i]=sum2[i-1 ]+a[i].value; } int ans=0 ; for (int i=1 ;i<=n;i++){ if (sum1[i]==sum2[i]){ ans++; } } printf ("%lld\n" ,ans); } signed main () int t=1 ; while (t--)solve (); return 0 ; }
G. The Witchwood 题目描述 题目分析 签到,也没啥好说的,就是加出前k大的数。
标程 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> #define int long long using namespace std;const int inf = 0x3f3f3f3f ;int n, m, t, res = inf; const int N = 1050 ;int a[N];signed main () int n, k; cin >> n >> k; for (int i = 1 ; i <= n; i++) cin >> a[i]; sort (a + 1 , a + n + 1 ); int sum = 0 ; for (int i = n; i >= n - k + 1 ; i--) sum += a[i]; cout << sum; return 0 ; }
K.Scholomance Academy 题目描述 题目描述比较长,也不截全了。
题目分析 这题是题是题面巨长,但是答案巨简单的一题,讲的是一个机器学习的问题。我们只需要设置 θ 的值扫过去,然后积分算面积即可,没有用到啥算法。
标程 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> #define int long long #define endl "\n" using namespace std;const int N = 1e6 + 10 ; struct V { char op; int v; } a[N]; int n, tn, fn, tp, fp;double ans, preX; bool cmp (V& a, V& b) if (a.v == b.v) return a.op < b.op; return a.v < b.v; } signed main () ios::sync_with_stdio (false ); cin >> n; for (int i = 1 ; i <= n; i++) { cin >> a[i].op >> a[i].v; if (a[i].op == '+' ) fn++; else tn++; } sort (a + 1 , a + n + 1 , cmp); for (int i = n; i >= 1 ; i--) { if (a[i].op == '+' ) tp++, fn--; else fp++, tn--; ans += 1.0 * tp / (tp + fn) * (1.0 * fp / (tn + fp) - preX); preX = 1.0 * fp / (tn + fp); } cout << setprecision (10 ) << fixed << ans << "\n" ; }
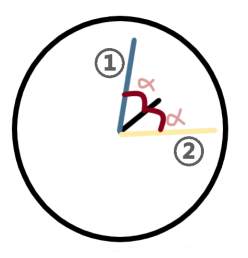
题意分析 题意: 一个时钟,时针走一圈就是一天,现在给定时针走一圈要 $H$ 小时,分针走一圈要 $M$ 分钟,设 $α=\frac{2πA}{HM}$,求一天中时针和分针夹角小于等于 $α$ 的时刻有几次。
这题首先有如下几个注意点:
切入点: 一般会最先想到用追及问题的角度去做,但是这样就有两个变量(涉及到分针和时针两个对象),所以我们可以选择将时针作为参照物 (参照物静止不动),运用相对速度只对分针这一个对象做分析。
两者绝对速度: $v_{h绝对}= \frac{2π}{HM}$ ,$ v_{m绝对}=\frac{2π}{M}$
分针相对速度: $v_{m相对}=v_{m绝对}-v_{h绝对}=\frac{2π}{HM}*(H-1)=(H-1)v_{h绝对}$
即分针相对于时针以 $H−1/min$ 的恒定速度运动。
要使两者之间夹角小于等于α,也就相当于追及问题中的两针“路程差”≤α,而此处因为时针作为参照物了,所以也就转化成了分针的“路程”$≤α=\frac{2πA}{HM}=A*v_{h绝对}$
因此我们可以写出一个关于时间 $t∈[0,HM)$ 的不等式:
$t\times (H-1)v_{h绝对}\ mod\ HM ≤ |α|=|A∗ v h 绝 对 *v_{h绝对}∗v $
$t\times (H-1)\ mod\ HM\le |A|$
根据剩余系定理三:
所以为了满足互质,可将不等式两边同除以 $g =\gcd(H-1,HM)$ ,不等式可等价为:
$t\times \frac{H-1}{g}\ mod\ \frac{HM}{g} \le |\frac{A}{g}|$
$\frac{-A}{g}\le t\times \frac{H-1}{g}\ mod\ \frac{HM}{g}\le \frac{A}{g}$
————注意:此处t的取值范围也同时从 $[ 0 , HM )$ 缩小到 $[ 0,\frac{HM}{g})$ —————
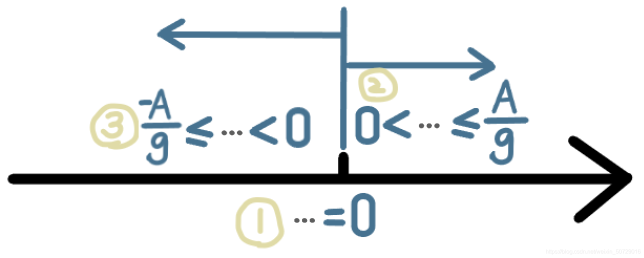
下面就只需求解出 t 的整数解的个数,即为满足条件的时刻的次数。我画在数轴上会比较直观。只需求出正半轴有几个整数解,然后个数 $\times 2$并且加上零解。
正半轴:因为要mod之后余数$≤\frac{A}{g}$,因此一共有余数为$1,2,3…\frac{A}{g} $ 的共计 $\frac{A}{g}$ 个解,并且这些解中没有重复的,即t的值与余数取值一 一对应,下证:
令$a=\frac{H-1}{g}$ ,$b=\frac{HM}{g} $
假设存在$t_1$和$t_2$ 两个不同的值满足:$t_1\times\ mod\ b ≡ t_2\times a\ mod\ b$ 且 $t ∈ [ 0 , b ]$ 因此根据同余定义,易证$t_1=t_2$ 与假设矛盾,因此每个t的解所对应的余数一定是各不相同的。
所以在 $t∈[ 0 , \frac{HM}{g} )$ 的范围内一共有 $2\times (\frac{A}{g})+1$个不同整数解。把范围还原到 $ [ 0 , HM ) $,就共有 $g\times[2\times(\frac{A}g)+1]$ 个不同的整数解,也就是本题答案之一。
有一种情况需要特判,就是当 $A=\frac{HM}{2}$,这时 $α=π$ ,$t ∈ [ 0 , HM )$ 中的每个整数都满足条件,故答案为 $HM$
标程 然后标程就巨短
1 2 3 4 5 6 7 8 9 10 11 12 #include <bits/stdc++.h> using namespace std;#define ll long long ll h,m,a; int main () scanf ("%lld%lld%lld" ,&h,&m,&a); ll g=__gcd(h-1 ,h*m); if (a==h*m/2 ) printf ("%lld" ,h*m); else printf ("%lld" ,g*(2 *(a/g)+1 )); return 0 ; }
小结 希望能和sigma姐姐一起进步,争取下次能vp到铜首水平。