之前 CS:APP 没有好好学，今天下定决心来重新看一遍，并把实验好好做一遍以巩固自身。

信息存储

数字表示

二进制：区别于我们平时计数使用的十进制，二进制使用的是逢二进一原则，而我们的十进制则是逢十进一，比如我们十进制的 9+1 中的 9，答案应该是十，但是十应该进一，因此得出了我们常规的答案 10。在二进制里面，每一位只要大于等于 2 则都要向高位进一。为了方便表示，还衍生出了二进制的子类，比如八进制，十六进制等，主要是二进制向这R

些进制转换较为容易，而计算机平时又都处理二进制数据，因此就出现了这些常见的进制计数。

信息存储

大多数计算机使用的都是8位（在计算机中，除特殊说明外，一位均指的是二进制的位）的块，或者叫字节，字节是作为计算机可寻址的最小单位。一般来说我们并不习惯于将一个字节写成八位二进制的数，而是会写成两位十六进制的数。十六进制与二进制之间的转换也会十分容易，举个例子：

1
2
0x99->0b10011001
0x88->0b10001000

我们可以发现我们并不用像十进制那样权值相加或者是除二取余那么麻烦，我们把一位十六进制视为四位二进制即可，这样我们在转换的时候就是直接每一位分别转了，可以看出十分的方便。

字数据大小

每台计算机都有一个字长，字长为计算机 CPU 一次能处理的最大数据，也有一种说法是能表示的最大内存。其实意思是差不多的，比如我们都知道 32 位的计算机最多能装 4GB 的内存，再多它也是只能使用这么多的内存，那是因为 CPU 要访问内存的时候，也只能使用一个 32 位的数据来表示地址，32位的数能表示的数的个数也就是 2^32 这么多，而地址指示的单位是字节，所以最多就是 2^32 字节，那就是熟知的 4GB 了。

C 语言中 sizeof() 会返回一个对象所占的字节数，我们对比输出下 32 位机子和 64 位机子的各个基本数据类型所占的字节数。我们不必找两个机子，只需要在 64 位的机子上分别编译 32 位和 64 位的程序即可。

1
2
3
4
5
6
7
8
9
10
11
#include<stdio.h>

int main(){
    printf("char:%d\n",sizeof(char));
    printf("short:%d\n",sizeof(short));
    printf("int:%d\n",sizeof(int));
    printf("long:%d\n",sizeof(long));
    printf("char *:%d\n",sizeof(char *));
    printf("float:%d\n",sizeof(float));
    printf("double:%d\n",sizeof(double));
}

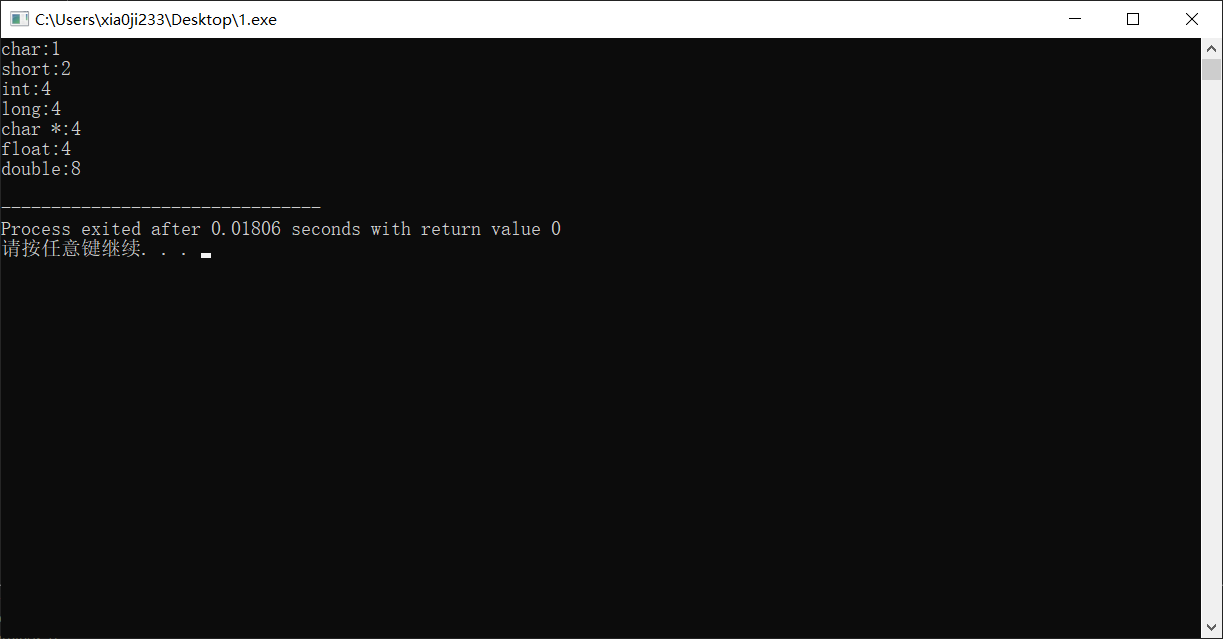
32 位的结果：

64 位的结果：

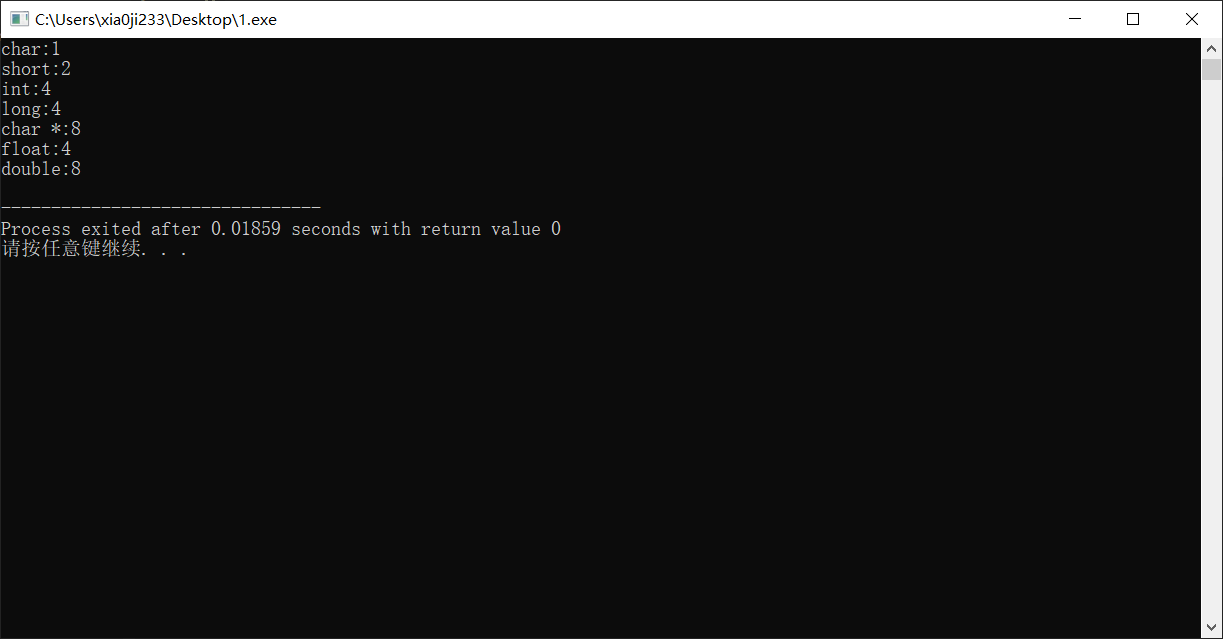
我们总结出如下表格

C声明 32位字节数 64位字节数
char 1 1
short 2 2
int 4 4
long 4 4
char * 4 8
float 4 4
double 8 8

其实有些时候， long 的字节数也会随机器字长有所变化的，只是好像某个版本区分了 64 位整数就叫 long long 而 long 地位与 int 一致了。但是除了这个问题，可以发现只有指针类型的数据会随着机器字长发生变化，这也如我们所说，机器字长决定了指针就多少位，决定了有多少个地址，能用多少内存，多出的内存机器就无法做区分了。

寻址和字节顺序

对于多字节的数据类型我们必须确定两点：

  1. 这个对象地址在哪里
  2. 这个对象中的字节按什么顺序排列

比如一个 int 它有四个字节，那么我定义 int a=0x12345678。首先它一定是连续排列的，因此我们确定一个 int 的地址只需要确定它的最高字节的位置即可确定整个 int 的位置。假如 int 的地址是在 0x100 的，那么它应该怎么排列这些字节呢？

我们最初可能按照惯性，认为它是按照如下方式存储的：

1
2
字节：12  34  56  78
地址：100 101 102 103

这个也很符合我们的书写规则，但是实时却恰恰相反，在现在大部分的机器中，它是反着存储的。也就是

1
2
字节：78  56  34  12
地址：100 101 102 103

这两种存储方式我们分别叫大端序和小端序。

  • 大端序：最高有效字节在低地址

  • 小端序：最高有效字节在高地址

在我们书写汇编语言的时候，要写一个值通常也是以小端序的方式书写的。

比如我给 eax 寄存器加上 0x12345678 你会发现它的字节码是：

1
2
mov    $0x12345678,%eax 
b8 78 56 34 12

我们通过定义以下的函数以十六进制来逐个显示内存中的字节。

1
2
3
4
5
6
void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}

其中 start 参数为该对象的起始地址，len 参数为显示的字节数，可以任意定义变量调用这个函数来查看这个对象在内存中的排布，理解浮点数的时候这个函数非常有用。

来查看下面的一个例子：

1
2
3
4
5
6
7
8
9
10
11
12
void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}
int main(){
    int x=0x3039;
    show_bytes(&x,sizeof(x));
    float y=x;
    show_bytes(&y,sizeof(y));
}

可以发现浮点数的输出在整数形态下为 0x4640E400。与整数的存储有着截然不同的结果，但是我们对这个结果的二进制适当移位就会发现它们有13个相匹配的位。

1
2
3
4
  0   0   0   0   3   0   3   9
0000000000000000001000000111001
            4   6   4   0   E   4   0   0
         01000110010000001110010000000000

我们也可以看到13个位刚好就是 int 形式下的低 13 位，这并不是巧合，大家可以试试看其它数，并且可以看看它最多能匹配多少位的整数，但是要注意结论需要有一般性，特殊的数字符合并不能得出什么结论，只能说是特性。

表示字符串

字符串的定义就是一个以 null 字符结尾的字符数组，如果将字符串看成一个数据类型的话，那么它是以大端形式存储的，但是其实实际上应该说是数组是大端存储的。我们在书写的时候，一般下标 0 是最小的，但是我们习惯把它称为高位，高位在低地址便是大端序。比如 char s[]="1234"; 那么 s[0]='1',s[1]='2',s[2]='3',s[3]=4,s[4]=NULL。请注意末尾的空字节也会包括在字符串里面，但是我们算长度不会算上这个字节。在 gcc 编译器中，我们编译如下的程序：

1
2
3
4
5
6
7
#include<stdio.h>
char s[]="0123456789ABCDEF";
int main(){
    char buf[16];
    strcpy(buf,s);
    printf("%s",s);
}

编译器会发出可能存在溢出的警告，因为在拷贝的时候会多携带一个 0 字节过来，这在后面堆利用中也是很常见的 off by null 的手段。

再比如我们用这样的方式：

1
2
3
4
5
#include<stdio.h>
char s[]="0123456789ABCDEF";
int main(){
    printf("%d",sizeof(s));
}

运行我们也可以发现这个 char 数组占用了 17 个字节的空间。

布尔代数简介

布尔代数是一个建立在二元集合集合 G={0,1} 上的定义。

非

非0即为1，非非0即为0。

与

全1为1，不全1为0

或

全0为0，不全0为1

异或

相同为0，不同为1

结论

  1. 非0为1，非1为0
  2. 1与1为1，1与0为0，0与1为0，0与0为0
  3. 1或1为1，1或0为1，0或1为1，0或0为0
  4. 1异或1为0，1异或0为1，0异或1为1，0异或0为0

在C语言中也有一个类型是 bool，它们有特殊的运算符：

  • 与：&&
  • 或：||
  • 非：!

不一样的是，在进行这些运算的时候，统统会把参与运算的值转为 bool 类型，0 就是 0，不是 0 一律都是 1

C语言当中的位级运算

位逻辑运算

我们平时C语言的位运算会扩展到每一位，位之间独立地运算，我们可以把一个整数(int)视为32维的向量，每个维度为0或者1，对整数进行位逻辑运算相当于每一位分别做逻辑运算，每一位结果为新向量对应位的结果。在 C 语言中，以上逻辑运算对应的符号分别为：

  • 非：~
  • 与：&
  • 或：|
  • 异或：^

我们可以在只拥有非和其它任意一个双目运算来实现所有的位逻辑运算。

比如我不用异或实现异或的功能，那么就是：

一个为 1，一个为 0 那么为或者一个为 0，一个为 1 的情况都是 1，其余都是 0。我们知道与的特性就是只有全 1 的时候为 0，那么如果我其中一个取非了，再与还是1的话就说明一个为 1 一个为 0 了，两边都非一下，最后把符合条件的位或一下就能得到异或的结果了。

1
2
3
int xor(int x,int y){
    return (~x&y)|(x&~y)
}

那与和或，把非运用到位了它们两个也能运用自如自由转换。

比如我用与和非实现或，首先我对两个元素都非一下然后与起来，是不是就变成了：

全 0 为 1，其余为 0 了，这和或的全 0 为 0，其余为 1 差了什么？很显然结果反了，那么我就对结果再非一下，最后就变成了：

1
2
3
int or(int x,int y){
    return ~(~x&~y);
}

或和非实现与运算同理。

移位运算

这里分逻辑移位和算数移位，其实差不多，只不过逻辑移位适用无符号整数，算数移位适用有符号整数。

分左移和右移，分别用符号 << 和 >> 来表示，假设整数一共 w 位，右移 n 位表示丢弃低 n 位，原来的高w-n 位变为低 w-n 位，高 n 位变为0。左移 n 位表示丢弃高 n 位，原来的低 w-n 位变为高 w-n 位，低 n 位变为0。

逻辑移位

左移右移就是字面意思

算数移位

正数与逻辑移位一样，负数则会在右移的时候高位添1.

左移x相当于对该数乘 2 的 x 次方，右移相当于对该数除 2 的 x 次方取整。

当移位的位数大于等于该整数的最大位数，则会取模再移位。

整数表示

整数我们之前讲过了它的字节排布规律，但是对于负数计算机又将如何处理呢？

整数数据类型

我们先来看一张表格

C定义 最小值 最大值
char -128 127
unsigned char 0 255
short -32768 32767
unsigned short 0 65535
int -2147483648 2147483647
unsigned int 0 4294967295
long -9223372036854775808 9223372036854775807
unsigned long 0 18446744037709551615

我们可以很清楚地看到，有符号数在正数和负数的范围并不严格对称，这是为什么我们接下来再看。

无符号数的编码

无符号数的编码就是用一个固定长度的向量来表示，每个维度上的值取 0 或者 1，那么有

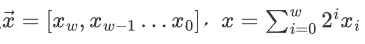
这个是我们最容易理解的。

补码编码

有符号数因为需要表示负数，因此它规定：最高位的权值为负。

也就是说若最高位为1，而我们知道，在等比数列 ai=2^i 中，数列的前n项和永远比第 n+1 项小 1，根据等比数列前 n 项和的公式。因此若最高位为1，那么其它位不管是是怎样都不会使这个数变为一个正数。而前 n-1 项可以表示 0~2^n-1 的范围，所以负数的范围就是-2^n+0~-2^n+2^n-1 也就是我们熟知的 -2^n~-1 再加上正数表示的 0~2^n-1 连起来的范围就是 -2^n~2^n-1 啦。

有符号与无符号数之间的转换

隐式转换按顺序遵从以下原则：

  1. 浮点数参与运算就是浮点数，出现过double则结果一定为double
  2. 若都是整数参与运算则结果也是整数
  3. 整数运算的结果为出现过的位数最大的整数，若最大的整数中有无符号类型的则结果无符号。

因此，如果

  • 运算中有 unsigned short 和 int 则结果为 int。
  • 运算中有 unsigned int 和 int 则结果为 int。
  • 运算中有 unsigned int 和 float 则结果为 float。

也就不一一列举了。

有符号与无符号的位于区别就是最高位的权值正负问题，比较的时候任意一方出现无符号则另一方也会变成无符号比较，所以如果我们做以下运算：

1
-1<(unsigned)1

会发现它结果为0.

因为 -1 的补码全为 0，转为无符号之后会变成无符号整数的最大值。

扩展一个数字的表示

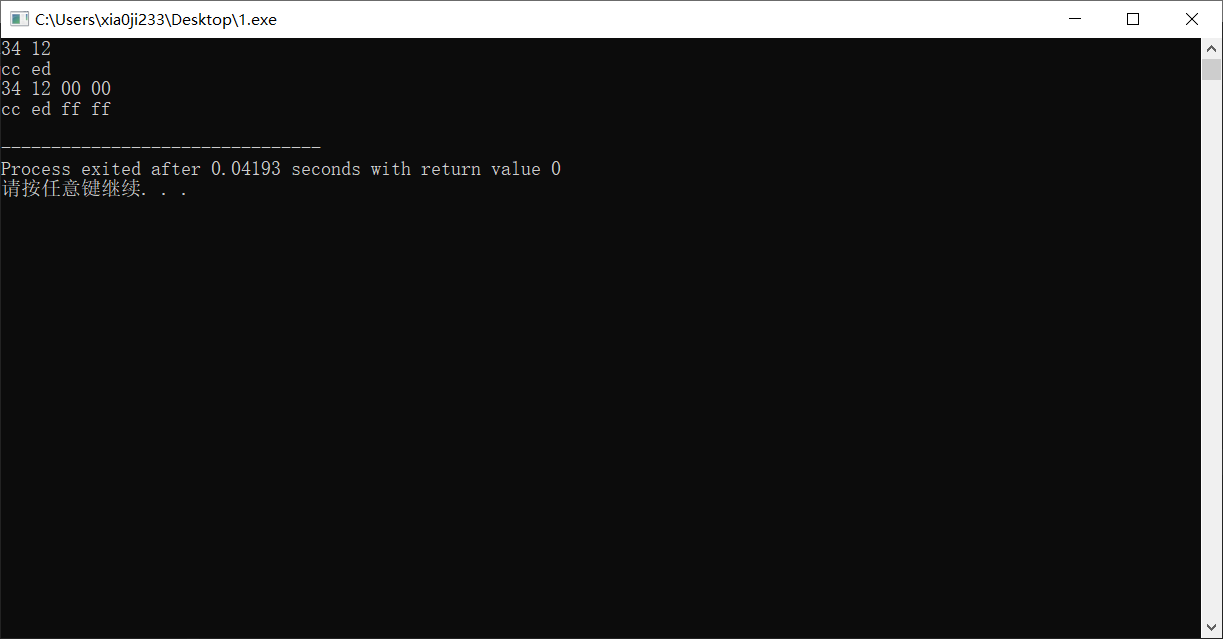
将一个位数较小的整数扩展为位数较大的整数非常简单，我们只需要在开头添加 0 即可，但是如果是负数，则需要开头添 1，我们运行以下代码试试看：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<stdio.h>
void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}
int main(){
    short x=0x1234;
    short y=-0x1234;
    show_bytes(&x,sizeof(x));
    show_bytes(&y,sizeof(y));
    int x1=x;
    int y1=y;
    show_bytes(&x1,sizeof(x1));
    show_bytes(&y1,sizeof(y1));
}

运行可以看到结果如我们所说。

截断数字

有扩展，自然有截断，当运算的结果可能超出类型所能表示的最大范围的时候，就会发生溢出。

在无符号数或者正数当中，截断为 w 位的整数就相当于取模 2^w ，但是截断有负整数的时候就会发生意想不到的事情。比如负数最小值再减一那么做的运算就是：

1
2
3
 0x80000000
 0xFFFFFFFF
0x17FFFFFFF

显然多了一位，高位被截断，最终结果为 0x7FFFFFFF ，两个负数相加结果得出了正数，这显然超出了我们的认知范围。这个我们叫它负溢出。再看一个例子：正数的最大值加 1

1
2
3
0x7FFFFFFF
0x00000001
0x80000000

结果是负数的最大值，两个正数相加得出了负数，显然也不合理，这个我们叫他正溢出，但是正溢出并没有发生截断，而负溢出是由截断引起的。

计算机历史上，有很多安全漏洞都是因为有符号和无符号的正数引起的

无符号乘法

对于乘法有 x*y=(x*y) mod 2^w 其中 w 为 x 和 y 的位数。因为 x 和 y 相乘可能得到最大 2w 位的整数，因此会发生截断，对于无符号来说，截断就相当于对 2^w 取模 。

补码乘法

这个乘法就相当于先像无符号乘法，乘出来截断之后再转为补码就是结果。

乘常数

因为我们知道一个特性：移位运算相当于对 2^x 做乘除法，因此利用这个特性我们能把乘法转成移位运算，执行乘法指令的时间比其它指令时间要长的多，因此很多编译器在编译常数乘法的时候会把常数二进制拆开然后分别相乘相加。

比如乘9：

1
2
9=0b1001
x*9=x*8+x*1=(x<<3)+(x<<0);

但是我们会发现一个问题：如果1的位数很多那就相当于要做很多次移位和加法，最后的复杂度可能跟乘法指令差不多，但是我们可以通过另外一种姿势避免这个问题：

1
2
15=0b1111=0b10000-0b1
x*15=x*16-x*1=(x<<4)-(x<<0);

通过借一个高位，其余位权值取反之后再加1的方式避免了进行大量的运算。

除2的幂

对于2的幂，非常简单，右移运算即可，但是需要注意：除法没有分配律，所以乘常数的方式并不适用于除法。除法会向零取整，比如算出来结果为 3.5 则会变成 3，算出来结果 -3.5 则会变成 -3。

浮点数表示

显然整数并不能满足我们平时的需要，平时还需要进行大量的浮点数运算，达到太阳的质量，小到电子的质量，都需要能在计算机中表示。而这个范围要用整数的思路表示显然是不行的，因此我们需要有特殊的表示方法。

二进制小数

我们都知道十进制的小数，小数点左边的数字位的权值从 10^0 开始，指数逐位递增，而小数点右边的数字的位的权值从 10^(-1) 开始，逐位递减。

二进制同理，只不过权值的底数都变成了 2。

IEEE浮点数表示

这个标准规定的浮点数用如下方式表示：

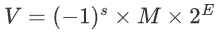
里面包含了

  • 符号(s)：1 表示负数，0 表示正数
  • 尾数(M)：是一个二进制的小数，取值范围为 [1,2)
  • 阶码(E)：为浮点数加权。

其实这个定义就相当于二进制的科学计数法，想想原来科学计数法的定义是不是能更清晰地理解它了呢？

讲完理论来讲点实际的：

我们知道实际上我们经常用的浮点数有两类，一类是 float 一类是 double，float 为 32 位，double 为 64 位。

  • 对于 float，最高位表示符号位，第 2 到第 9 位表示阶码，第 10 位到第 32 位均为尾数
  • 对于 double，最高位表示符号位，第 2 到第 12 位表示阶码，第 13 位到第 64 位均为尾数

我们具体以 float 来分析：

第一位是符号位没啥大问题。后面的八位是指数，这个指数需要能表示无穷大，也要能表示无穷小，因此指数必须有正有负。我们定义一个数 Bias=2^(k-1)-1 其中 k 为阶码的位数，在 float 中，这个值为 127，在 double 中，这个值为 1023。阶码实际值 E=e-Bias，其中 e 表示阶码本身的无符号二进制的数值。然后就是这个尾数了，因为我们的范围是 [1,2)，在这个范围内的小鼠，不难发现小数点前有一位一直是 0，因此这个 0 我们就不必多花一位存储它了，因此我们的尾数都是小数点后的值。

如果一个 32 位浮点数在内存中的二进制表示如下：

1
2
bin:0b01000000010000000000000000000
hex:0x40400000

那么可以发现它是正数，阶码为 128，尾数为 100000……，因为小数点后面的0都能忽略，因此尾数实际就是 1。然后注意这个阶码并不是真正的实际值，这只是它表面上看上去的值，再给它减去一个 127 之后可以发现指数为 1。小数位数因为有一个隐含的 1，所以它的实际值为 1.1，十进制值就是 1.5，所以最后结果就是 1.5*2^1=3。

然后我们再运行程序看看 3 的字节显示。

1
2
3
4
5
6
7
8
9
10
11
#include<stdio.h>
void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}
int main(){
    float x=3.0;
    show_bytes(&x,sizeof(x));
}

运行之后可以发现与我们上面书写的十六进制值一致。

浮点数还有 3 中表示值的情况。

  1. 规格化的值：这是最普遍的情况，阶码位不为全 0 也不为全 1.
  2. 非规格化的值：当阶码位全为 0 的时候，表示非规格化的值，这个非规格化的意思就是跟我们上面介绍的规律稍稍有点不一样，此时尾数是不带隐含的 1 的，也就是说它的有效数字直接是从尾数开始的，因此它和阶码位模式为00000001 的指数一样，但是有效数字多一个小数点前的 1，因为这样表示能够使得非规格化数值向规格化数值转化更为平滑。
  3. 特殊值：包括 INF 和 NAN，阶码位全为 1 的时候，若尾数全为0，则得到 INF，若不全为 0 则得到 NAN。

舍入

浮点数因为表达的不是一个具体的数，只是一个近似值，因此在精度不够的情况，只能选择舍掉一些精度保证能够存储。如何舍入便成为了一项难题，目前一共有四种舍入方式：下面我们给出一些例子

方式 1.40 1.60 1.50 2.50 -1.50
向偶数舍入 1 2 2 2 -2
向零舍入 1 1 1 2 -1
向下舍入 1 1 1 2 -2
向上舍入 2 2 2 3 -1

后面三个方式还好，应该都能理解，主要是这个向偶数舍入，它首先满足：被舍入的值不超过最小单位的一半则丢弃，若超过一半则加上一个最小单位，若等于一半则一定会使得舍入的结果为偶数个最小计量单位。

浮点运算

在进行浮点数加减法的时候，首先需要对阶，小阶向大阶对齐，然后尾数相加。由于特殊值的存在，浮点数加减法并不满足交换规则，因此它不是一个阿贝尔群，很多整数规律不适用。

比如最经典的：

1
1+1e111-1e111!=1e111-1e111+1

小结

这里来回答一下之前遗留的一个问题，那就是为什么整数转为浮点数之后会有部分位相匹配。其实不难发现是因为浮点数的尾数基本是和原二进制的值一致的。比如下面的一个数

1
1001001010101

转为浮点数之后就会变成

1
1.001001010101*2^12

这个尾数是与原二进制的值一致的，想到这里你肯定明白了之前的那个问题了。

CSAPP:datalab

终于到了最激动的实验环节了，原先我对这本书并没有很深的了解，直接上手做的实验，不会就搜，现在看完一遍之后感觉理解很多，做实验基本也是畅通无阻。

用给定的运算符实现函数的功能，解压得到源码之后在 bits.c 中编写自己的代码，然后要查看结果可以使用如下命令：

1
2
$make
$./btest

实验规定并非强制，但是想获得提升还是严格遵守它给定的条件。

bitXor

1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
      return 2;
}

只允许使用位运算 ~ 和 & 实现按位异或，这个我们在上面有写过，只不过没有合在一起，稍微转换一下即可，反正实现的思想就是要位之间不一样才返回 1。

答案

1
2
3
int bitXor(int x, int y) {
    return ~(~(~x&y)&~(x&~y));
}

tmin

1
2
3
4
5
6
7
8
9
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
    return 2;
}

获得整数的最小值，最小值就是我们喜闻乐见的 -2147483648 啦，但是我们稍微转换一下思路，最小就是最高位一个0，用个 1，然后移位运算把它移到最高位即可。

答案

1
2
3
int tmin(void) {
    return 1<<31;
}

isTmax

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
    return 2;
}

判断 x 是否为最大值，最大值应该是最小值取反，然后判断是否一样我们使用异或运算，异或只有在两边相等时才返回 0，我们用非运算符反一下就可以了。

答案

1
2
3
int isTmax(int x) {
    return !((~(1<<31))^x);
}

allOddBits

1
2
3
4
5
6
7
8
9
10
11
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
    return 2;
}

判断 x 是否奇数位上全为 1。全 1 我们直接用一个立即数好了 0xAAAAAAAA，然后与屏蔽偶数位之后判断是否相等即可。

答案

1
2
3
int allOddBits(int x) {
    return !((0xAAAAAAAA&x)^0xAAAAAAAA);
}

negate

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
    return 2;
}

实现对一个数取负，取负的话就是取反再加一即可。

1
2
3
int negate(int x) {
    return ~x+1;
}

isAsciiDigit

1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x){
    return 2;
}

判断一个整数是否在 ASCII 码的数字位置，再转换一下就是满足这个条件：

1
x-0x30>=0  && x-0x3a<0

我们的目标就是判断 x-0x30 是否为非负数，x-0x3a 是否为负数，也许需要考虑溢出，但是结果发现不需要，因为这个是两边判断的。

答案

1
2
3
int isAsciiDigit(int x){//x-0x30>=0  && x-0x3a<0
    return !((x+(~0x30+1))&(1<<31))&!!((x+(~0x3a+1))&(1<<31));
}

conditional

1
2
3
4
5
6
7
8
9
10
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
    return 2;
}

相当于实现运算 x?y:z，如果 x 为 0 则返回 x，如果不为 0 则返回 y。

我们先把 x取值变为只有 0 和 -1。用掩码的思路，如过结果为 -1 则说明位模式全为 1，相与的结果就是另一个数本身，如果是 0 则不论与谁结果都是 0，我们让 x 与 y，让 ~x 与 z，最后得到的两个值或起来即可。x 如果是 -1 则返回 y ，如果是 0 则返回 z。得到 x 我们只要非两次，再取负即可，就达到了我们的要求了。

1
2
3
4
int conditional(int x, int y, int z) {
    x=~(!!x)+1;
    return (x&y)|(~x&z);
}

isLessOrEqual

1
2
3
4
5
6
7
8
9
10
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  return 2;
}

实现一个小于等于的功能，这里需要注意的是不能直接相减，会有溢出。

因此我们选择先判断符号位，符号位一致再相减一定不会溢出，符号不一致则强行返回不一致的结果，一致则返回直接相减的结果。首先我们先拿两个变量保存符号的结果，然后再判断符号是否一致，一致则屏蔽符号的结果，不一致则屏蔽相减的结果。

这里好好再理解一下，仔细看 signx^signy 和 !(signx^signy) 如何起到屏蔽答案的效果。

答案

1
2
3
4
5
6
7
8
int isLessOrEqual(int x, int y) {//y-x>=0
    int signx=!(x&(1<<31));
    int signy=!(y&(1<<31));
    int sign=(signx^signy)&signy;//若不一致则返回y是否为非负数
    x=x&0x7fffffff;
    y=y&0x7fffffff;
    return sign|(!(((y+(~x+1))&(1<<31))))&(!(signx^signy));
}

logicalNeg

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
    return 2;
}

实现逻辑非的功能，我们这里需要研究一下 0 的特性，0 是除了 TMIN 以外的负数值等于自己本身的数了。然后再判断一下最高位即可。

答案

1
2
3
int logicalNeg(int x) {
    return ((x|(~x+1))>>31)+1;
}

howManyBits

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
    return 2;
}

这题挺难的，首先要想到一个二分，然后要注意正数需要多一位，负数不需要。假如我给了你 0x7fffffff，那么你肯定要 32 位，虽然我只有 31 位有效数字。我给你个 -1 那一位就够了，因为一位的范围就是 -1~0。

我们先判断高 16 位是否有 1，若有则判断高 16 位，答案加上 16，否则判断低 16 位。

再判断的 16 位中，判断高 8 位是否有 1，若有则继续判断高 8 位，答案加上8，否则判断低 8 位。

直到判完。我一开始想到了这个：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int howManyBits(int x) {
    int sign=!(>>31); 
    int b16=(!!((x>>16)&0xffff))<<4;
    x=x>>b16;
    x=x&0xffff;
    int b8=(!!((x>>8)&0xff))<<3;
    x=x>>b8;
    int b4=(!!((x>>4)&0xf))<<2;
    x=x>>b4;
    int b2=(!!((x>>2)&0x3))<<1;
    x=x>>b2;
    int b1=(!!((x>>1)&0x1))<<0;
    x=x>>b1;
    printf("%d %d %d %d %d %d %d\n",b16,b8,b4,b2,b1,x,sign);
    return b16+b8+b4+b2+b1+sign+x;
}

但是经过多方调试还是输给了 -1 这个测试点。后来想到如果负数则取反即可，然后符号位就默认给它加着上去即可。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int howManyBits(int x) {
    int sign=x>>31;
    x = (sign&~x)|(~sign&x);
    int b16=(!!((x>>16)&0xffff))<<4;
    x=x>>b16;
    x=x&0xffff;
    int b8=(!!((x>>8)&0xff))<<3;
    x=x>>b8;
    int b4=(!!((x>>4)&0xf))<<2;
    x=x>>b4;
    int b2=(!!((x>>2)&0x3))<<1;
    x=x>>b2;
    int b1=(!!((x>>1)&0x1))<<0;
    x=x>>b1;
    return b16+b8+b4+b2+b1+X+1;
}

整数阶段到此完结了就。

floatScale2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
    return 2;
}

就是返回一个浮点数乘 2。首先排除掉那些特殊值： NAN，INF 和 0，乘二返回指数 +1 即可，

答案

1
2
3
4
5
6
7
8
9
unsigned floatScale2(unsigned uf) {
    int exp = (uf&0x7f800000)>>23;
    int sign = uf&(1<<31);
    if(exp==0) return uf<<1|sign;
    if(exp==255) return uf;
    exp++;
    if(exp==255) return 0x7f800000|sign;
    return (exp<<23)|(uf&0x807fffff);
}

floatFloat2Int

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
    return 2;
}

实现一个类似是强制转换的东西吧，首先还是按照浮点数的规则把各个字段提取出来，然后特判移位就行了。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int floatFloat2Int(unsigned uf) {
    int s=uf>>31;
    int exp=((uf&0x7f800000)>>23)-127;
    int frac=(uf&0x007fffff)|0x00800000;
    if(!(uf&0x7fffffff)) return 0;
    
    if(exp>31)return 0x80000000;
    if(exp<0) return 0;
    
    if(exp>23)frac<<=(exp-23);
    else frac>>=(23-exp);
    
    if(!((frac>>31)^s)) return frac;
    else if(frac>>31) return 0x80000000;
    else return ~frac+1;
     
}

floatPower2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    return 2;
}

实现运算 pow(2,x)，返回结果为 int 虽然我们可以直接 1<<x，但是它要求浮点计算。

首先防止溢出先判断，因为是 2 的整数次方，所以它的结果就是 (exp+127)<<23，然后判断无穷小和溢出即可，这个比较简单。

答案

1
2
3
4
5
6
7
unsigned floatPower2(int x) {
    int INF = 0xff<<23;
    int exp = x + 127;
    if(exp <= 0) return 0;
    if(exp >= 255) return INF;
    return exp << 23;
}

需要注意，由于最后一个题目测试数据比较多，因此要修改时限才能通过。我也不知道我算法有什么问题，这 O(1) 的复杂度也不知道上哪优化去。

result

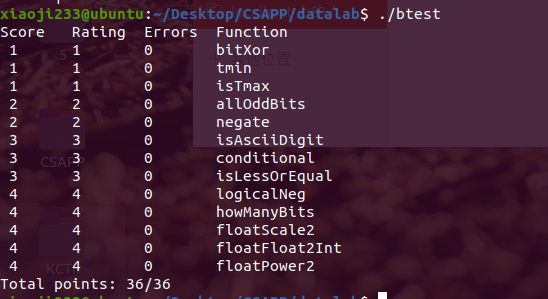
小结

啥也不说了 CSAPP 永远的神，入门二进制必备书籍，二刷都能感觉学到了很多以前没学到的东西，接下来没以前认真看的也都得去看一遍了。