RSA加密原理解析
今天来深度解析一下RSA加密
引言
还是最朴素的例子,Alice和Bob要在不安全的路线上发送信息,整条线路完全被窃听者Eve所知,如何让Alice和Bob安全地通信呢?如果这个例子略难懂,那换一个来讲,我要给别人寄个快递,我怎样让别人不知道我寄的是什么,一般情况下,如果没什么特殊情况,快递是不会被随便拆开查看的,但是也很难说,如果我给我实际要送的东西上把锁,那么即使我送的快递被拆开,没有钥匙也不会有人知道我送的是啥,而钥匙只有收件人拥有。
这就是非对称加密的一个例子了,一个人只有锁,另一个人有钥匙,可以这么说,当把锁关上的那一刻,寄件人都没办法打开去检查他寄的是啥,如果这个锁足够强大的话。
RSA加密
rsa主要是利用一系列的数学公式,让推导难以逆向分析,常见的有右移运算或者取模运算,RSA主要是使用取模运算。首先,我选择一个指数(e),让明文(m)进行这么多次的幂运算,再模上一个数(N),这也就得到了密文(c),这个密文难以逆向得到明文,因为取模运算不可逆,这个e和N是公开的,所有人都可以加密,也就是锁,但是钥匙只有自己拥有。
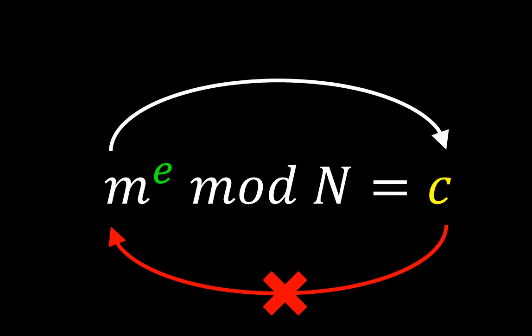
这里也先给出加密和解密的公式:

在这里d由一个公式算得:d相当于e在模φ(n)意义下的逆元。也就是它们满足这个公式:
$e\times d \ \ \text{mod}\ \ φ(n)=1$
RSA加密原理解析
为什么满足了这个关系就能通过上面的公式解密了呢?
通过e和d满足的关系我们可以得到这样的式子:
$e \times d=1+k*φ(n)$
k为任意整数。
$d=\frac{1+k*φ(n)}{e}$
这里还需要一个定理:欧拉定理
欧拉定理
这个算费马小定理的扩展吧,费马小定理的表达式如下:
对于任意整数a和任意质数p有以下式子成立:
$a^p$与$a$在$\ \text{mod}\ p$ 意义下同余,即$a^{p-1}\ \text{mod}\ p=1$
而对于任意质数,它的欧拉函数就是自己-1,欧拉函数的描述为
欧拉函数 是小于或等于n的正整数中与n互质的数的数目
而对于非质数,它一定可以写成若干个质数相乘,即
$n=p_1^{a_1}\times p_2^{a_2}\times p_3^{a_3}\times……\times p_n^{a_n}$
$a_i$为任意整数,$p_i$为任意质数,就是说,任何一个大于2的整数一定会有上式成立。
它的欧拉函数则是
$φ(n)=(p_1-1)p_1^{a_1-1}\times(p_2-1)p_2^{a_2-1}\times(p_3-1)p_3^{a_3-1}\times……\times(p_n-1)p_n^{a_n-1}$
那么欧拉定理的表达式是什么呢,那就是下面这个式子:
任意正整数a和p,有以下式子成立
$a^{φ(p)}\ \text{mod}\ p=1$
有了这个式子之后我们再代入上面那个式子,可以得到
$m^{e\times d}\ \text{mod}\ n=m^{1+kφ(n)}\ \text{mod}\ n$
这里需要用到一些简单的同余定理:
$a\times b\ \text{mod}\ n=((a\ \text{mod}\ n)\times (b\ \text{mod}\ n))\ \text{mod}\ n$
那么$m^{1+kφ(n)}\ \text{mod}\ n=m*(m^{φ(n)}\ \text{mod}\ n)^k\ \text{mod}\ n$
而括号里的表达式恒为1,最后结果就变成了$m$
可以发现,如果m不大于n,那么m的值应当是唯一的,而加密出现的中间产物$c$若没有$d$则永远无法推到得到$m$,这也就是RSA算法的核心了。
RSA密钥生成
讲完了原理之后我们来讲讲怎么生成RSA密钥,首先选取两个很大的质数p,q,这里得到n=p*q,那么容易得到n的欧拉函数$φ(n)=(p-1)\times (q-1)$
再任意选取一个质数e作为加密质数,也很容易算出解密指数$d=\text{inverse}(e,φ(n))$ ,inverse为求模逆元的函数。
$(e,n)$就是公钥,$(d,n)$就是私钥,这样我们的密钥就生成完毕了。
python代码实现
这里用到一个Crypto库,安装方法为:
1 | pip install pycryptodome |
demo:
1 | from Crypto.Util.number import * |
运行结果
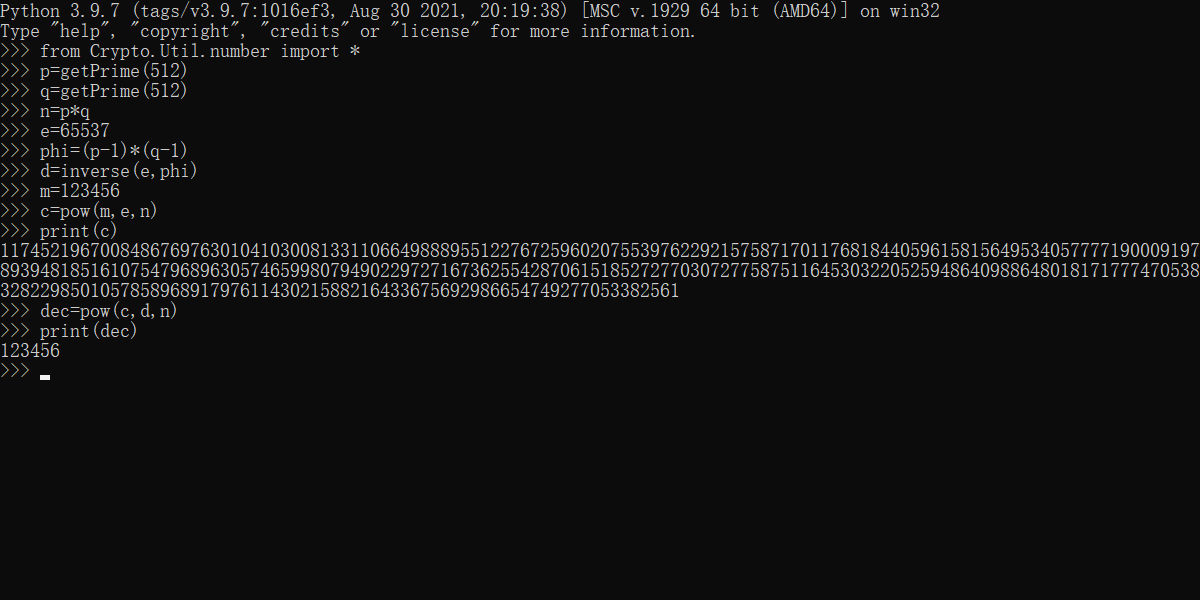
你也可以多取几个其它的数试试看,看看能不能得到一样的结果,因为质数随机生成,print(c)这一步不能保证一模一样,但是dec的值一定是和你输入的m一样的。