比赛遇到了新鲜的图论题，特此记录。

什么是Kruskal重构树？

\(\text{Kruskal}\) 重构树，和 \(\text{Kruskal}\) 算法的思想差不多，就是在这个过程中建出一个有着非常优秀的性质的数据结构，这是一个非常少见和小众的算法，但是如果碰到了合适的题目，就会体现出其优越性。

如何实现？

既然它叫 \(\text{Kruskal}\) 重构树，那么它必然与 \(\text{Kruskal}\) 有着密不可分的联系。首先我们回顾一下 \(\text{Kruskal}\) 最小生成树是怎么实现的，先将所有边按照权值排序，然后再从小到大添加边，如果添加边的两个顶点都在生成树当中则跳过这条边，直到添加过n-1次算法结束。

我们在添加边的时候构造一棵这样的树：当边e被添加时，e的两顶点一定在不同的生成树内，因此将两个顶点所在的树用一个点连接起来，点的权值为这条边的权值，这个点的权值表示了什么呢？就是这两个子树上，其中一个子树所有的顶点到另一个子树的所有顶点中经过的边的最大值的最小值为这条边的边权。

首先先解释一下什么叫最大值的最小值，这句话可能有点抽象，那我具体举一个例子。我一个节点从 \(u\to v\) 有可能经过多条边，这里面的最大值是我要计算的，而可能不止这一种走法，我现在希望这个最大值最小，这就是所谓的最大值的最小值啦。最大值指的是一条路径的最大值，最小值指的是所有路径中的这个值最小。

其次，很容易证明我们得到的树是一颗二叉树，因为对于n个点，每次我都是添加根节点连接两个子树或者节点，也很容易证明叶节点都为原图中的节点，因为我们只为这些节点不停地添加父亲而没有给他们儿子，自然就是叶子节点啦。

exp

exp(指example

举个例子，下面这个图。

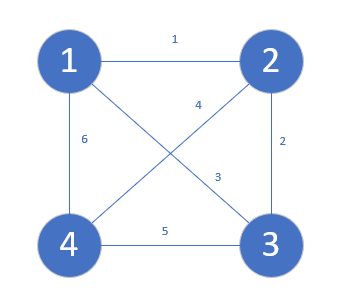
第一步，我们先选择1和2，发现不在同一集合，选择添加，我们新建一个节点来作为它们的父亲，它的点的权值为1，这里我换个颜色避免引起歧义，这里的1表示值而不是编号。

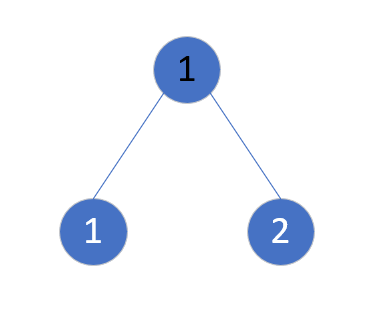
重复第一步，找到2，然后。

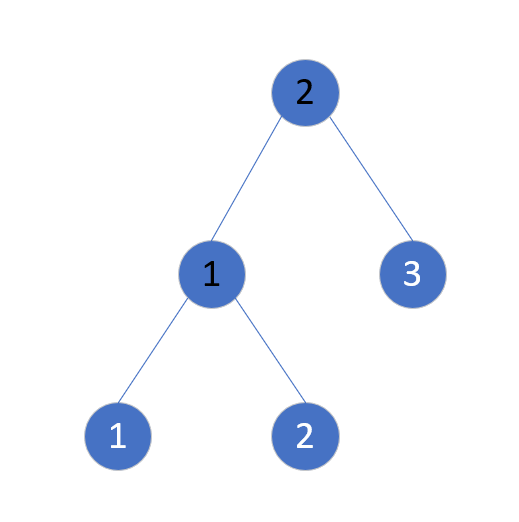
然后找到权值为3的点，发现1，3同属于一个树，跳过。再找到4，添加，得到下面这张图。

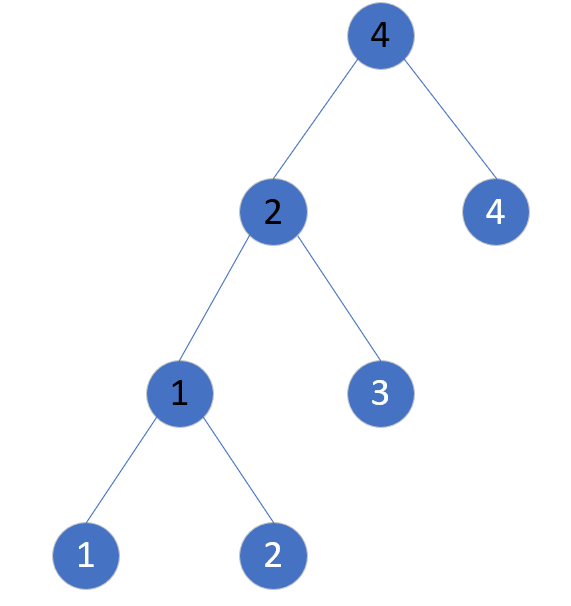
我们来看看符不符合我们上面总结的那个结论。

1和2我们走过的最短路径显然就是1；1到3我们需要走过路径最大值的最小值是2，虽然我能一步到达，但是先走2，再走3我们的路径长度为 \(\to 1\to 2 \to\) 显然这样走过的最长的路的最小值就是2了，可以发现1和3由根节点权值为2的点连接，也没问题，同理其它任何四个点两两之间都符合这个规律。

在实现上面我们可以通过LCA来快速查询两个点之间的最大路径的最小值，因为也可以发现两个点之间的LCA的权值就是我想要的答案，这一部分可以倍增预处理然后打到一次 \(log_2n\) 的复杂度。

有什么用？

这应该是我们最应该关心的问题了，学了一个数据结构应该想办法加以利用。来看一道经典例题：

给出n个点，m条边构成的无向图，要求指定两点，算出它们之间的最短路径值。

这题很容易知道可以使用单源最短路算法，但是我们也会想到动态规划。因为我到了一个点之后，我不需要关心这个点是怎么到的，这个叫无后效性，即前面的决策不影响后面的答案。

那我们对此题稍微改一下：要求求出所有我经过路径最大值的最小值是多少？

这题显然，也是无后效性我们只需要一步步往前推然后保存最大值即可。但是问题来了，如果我再加上多个询问呢？那么此时算法的时间复杂度将加上n倍，一次处理相当于进行一次的 \(\text{dijkstra}\)，\(O(nlog_2n)\)的复杂度，妥妥的超时。如果我们选择 \(\text{Kruskal}\) 重构树预处理，再加上加上LCA，把一次询问的复杂度降低到 \(O(log_2n)\) ，那么最终得到的算法复杂度就会低很多了。

例题

直接拿上ICPC2021上海站的I题——Life is a game

题目描述

Life is a game.

The world can be regarded as an undirected connected graph of \(n\) cities and mmm undirected roads between the cities. Now you, the life game player, are going to play the life game on the world graph.

Initially, you are at the \(x\)-th city and of \(k\) social ability points. You can earn social ability points by living and working. Specifically, you can earn \(a_i\) social ability points by living and working in the \(i\)-th city. But in this problem, you cannot earn social ability points duplicatedly in one city, so you want to travel the world and earn more social ability points. However, the roads are not easy. Specifically, there is an ability threshold \(i\)_iwi​ for the \(i\)-th road, you should be of at least \(w_i\) social ability points to go through the road. Moreover, Your social ability point will not decrease when passing roads but just need to be at least \(w_i\)​ if you want to go through the \(i\)-th road.

So as you can see, the life game is just living, working and traveling repeatedly. There are \(q\) game saves. For each game save, the initial city and social ability point is given and the player has not lived or worked in any city. Now you, the real life game player, need to determine the maximum possible number of social ability points you can have in the end of the game and output it for each given game save.

这里来解释一下这个题意。

就是说有一个 \(n\) 点 \(m\) 边的无向带权图，每个点上有权值。当你经过一个点，你能获得一定能力值，每个地方的能力值只能获得一次，只有能力值不小于边权我才能通过这条边到达另一个点。给定起点和初始能力值，问你最后最多有多少能力值。

所以，我们能不能到达另一个点取决于整条路经的最大值是否大于我的能力值，若大于则我不能通过这条路到达该点，如果该最大值最小，则以我目前能力值无法到达该点。

我们就使用 \(\text{Kruskal}\) 构造树，寻找它的祖先节点，可以证明，它祖先节点一定不是叶节点，所以如果我的能力值大于该祖先节点的值，那么我可以任意访问以这个祖先节点为根节点的任意节点，能力值可以直接加上这么多，然后再去寻找祖先节点，直到连它的父亲都无法到达或者是当前节点已经是根节点了，那就结束，那么我最终获得的能力值就是当前节点为根节点的子树的所有能力值之和加上初始值。

以某某节点为根节点的子树能力值之和可以通过 dfs 在 \(O(E)\) 的复杂度得出，排序+ \(\text{Kruskal}\) 构造树 \(O(E)+O(Elog_2E)\) 的复杂度。寻找根节点可以用预处理倍增查询的方式去得到。这样最终我们每次查询的复杂度就是 \(O(log_2n)\) 的复杂度。在本题我们可以认为它都是 \(n\) ，因为它们的最大值都是一样的，这样的复杂度最终能被接受。

这里给出我写的程序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include<bits/stdc++.h>
#define maxn 100005
#define int long long
//int不够直接int改long long
using namespace std;    
struct eee{
    int from;
    int to;
    int w;
    void read(){
        cin>>from>>to>>w;
    }
    bool operator <(const eee &a){//重载小于号便于排序
        return w<a.w;
    }
}e[maxn<<1];
int v[maxn<<1],root[maxn<<1],fa[maxn<<1],value[maxn<<1],a[maxn<<1],dep[maxn<<1],n,m,q,cnt;
int lca[maxn<<1][30];//这里忘开两倍内存导致2小时的TLE RE WA各种的问题。
//v表示节点权值，value表示子树a和，a表示该点的能量 
struct ee{
    int to;
    int next;
}edge[maxn<<3];
inline void add(int x,int y){
    edge[++cnt]={y,root[x]};
    root[x]=cnt;
}
int find(int x){
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void Kruskal(){
    for(int i=1;i<=2*n-1;i++)fa[i]=i;//初始化集合
    int j=0;
    for(int i=1;i<=m;i++){
        int from=e[i].from,to=e[i].to;
        from=find(from),to=find(to);//寻找并查集
        if(from==to)continue;
        v[++j+n]=e[i].w;//新建一个点，点权为该边边权，并连接这两个点
        add(from,j+n);//添加两个边。
        add(j+n,from);
        add(to,j+n);
        add(j+n,to);
        fa[from]=fa[j+n];//让这两个点的父亲都指向这个节点，这其实相当于一个集合的合并。
        fa[to]=fa[j+n];
        if(j==n-1)break;//寻找到n-1条边之后则直接退出
        
    }
}


int dfs(int now,int father){
    int ans=a[now];
    fa[now]=father;
    lca[now][0]=father;
    for(int i=1;i<17;i++){
        lca[now][i]=lca[lca[now][i-1]][i-1]//直接整，暴力出log_2(1e5)
    }
    for(int i=root[now];i;i=edge[i].next){//朴实无华的深搜
        int to=edge[i].to;
        if(to==father)continue;
        ans+=dfs(to,now);
    }
    value[now]=ans;//保存该节点为根节点时的所有子孙节点上的能力值
    return ans;
}
void sync(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
}

signed main(){
    //freopen("1.in","r",stdin);
    sync();
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=m;i++){
        e[i].read();
    }
    //以上为输入
    sort(e+1,e+1+m);//边按照权值排序
    Kruskal();//重构树
    dfs(2*n-1,0);//深搜填value，获得以每个节点为根节点能获得的能力值，顺便处理一下LCA
    v[0]=1e18;//防止到0之后无法终止递归
    while(q--){
        int x,k;
        cin>>x>>k;
        int t=x;
        int now=value[x]+k;
        while(1)
        {
            int las = x;
            for(int i = 20;i >= 0;--i)
            {
                int fa = lca[x][i];
                if(now >= v[fa]) x = fa;
            }
            if(x == las)break;
            now = value[x] + k;
        }
        cout<<now<<endl;
    }
    return 0;//完结撒花
}

程序注释提到了，咱因为数组越界查了两个小时的错误，硬生生没看到LCA没有开两倍的内存。

又一图论算法收入囊中，挺开心的。