最近花点时间看了看网络流，也深度地学习了一下网络流的各个算法，虽然还有一个没学，但是不影响。

概念引入

首先我们要先理解一下什么是网络，网络与有向图虽然长得一模一样，但是概念略微不一样，首先网络的边权不代表路径长度，代表流量或者花费。

  1. 源点：入读为0的点，只出不进
  2. 汇点：出度为0的点，只进不出

在网络中，对于非源点和汇点的所有点，需要满足流入流量之和等于流出流量之和，中间节点不存储任何流量，任何一条边的流量受限于自己的容量限制。

于是有的人就想要求出：这张网络运作起来的时候，总流量最大能有多少。由于容量限制比较复杂，似乎不容易规划一个最佳方案。

such as:

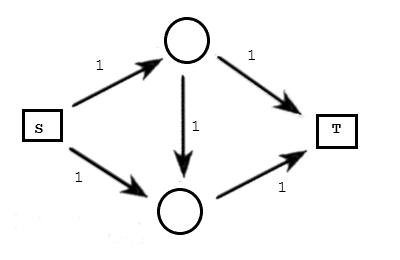
在这里，很容易得出 $s\to t$ 的最大流量就是2，上面一条路，下面一条路，边上的限制都是1，因此总流量为2。这里我们再给出两个概念：

  1. 增广 :在现有流量基础上发现新的路径,扩大发现的最大流量(注意:增加量不一定是这条路径的流量,而是新的流量与上次流量之差)
  2. 增广路:在现有流量基础上发现的新路径.(快来找茬,和上一条有何不同?)

因此我们有了第一个算法：FF。

虽然一般来说基本通不过测试点，但是还是有必要学的。

FF算法

从源点开始寻找增广路，如过找到那么整条路径的流量减去整个路径上的最小流量，然后重复寻找增广路，直到找不到增广路为止，最大流即是每次增广路减少的流量的和，这个结论是很容易证明的，所以咱就不证了。

很有幸，咱还是写过了这个算法，每次 $\text{dfs}$ 得到一个增广路，这个算法过得了图为树时候的最大流，但是过不去标板，标板的数据量才200个点，还能 TLE 很多点。

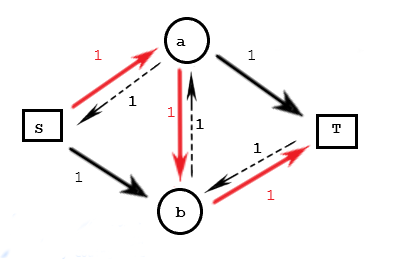
但是有一个问题，如果我一开始走了错误的路线，比如上面的图中，假如我走了中间那条路，那么就会导致接下来找不到增广路了，所以我们在走的时候会增加反悔功能，这条反向边就是防止走了错误路线给你反悔用的，假设你走了 $s\to a \to b\to t$ ，那么此时图变成这样：

那么在往下走的过程中我就能经过 $s \to b\to a\to t$，然后到达汇点。中间这条边经过两次，变回一开始的样子，相当于就是没走，这个反向边添加在所有的网络流算法都会用到，因此一定要理解。

这里给出练习这个算法的板子吧——P3931

我写的程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
struct eee{
    int next;
    int to;
    int w;
}edge[maxn<<1];
int r,n,cnt=1,root[maxn],fa[maxn],dest[maxn];
stack<int>path;
inline void add(int x,int y,int w){
    edge[++cnt]={root[x],y,w};
    root[x]=cnt;
}

void dfs(int u){
    for(int i=root[u];i;i=edge[i].next){
        int to=edge[i].to;
        if(fa[u]==to)continue;
        fa[to]=u;
        //edge[i^1].w=0;
        dfs(to);
    }
    if(!edge[root[u]].next&&u!=r){
        dest[u]=1;
    } 
}

int find_path(int now,int from,int flow){
    if(dest[now])return flow;
    int qw=0;
    for(int i=root[now];i;i=edge[i].next){
        int to=edge[i].to,w=edge[i].w;
        
        //printf("to is %d w is %d\n",to,w);
        if(to==from)continue;
        if(w==0)continue;
        path.push(i);
        qw=find_path(to,now,min(flow,w));
        if(qw==0)continue;
        break;
    }
    return qw;
}

void maxflow(){
    int ans=0;
    while(1){

        int l=find_path(r,0,0x7fffffff);
        if(l!=0&&l!=0x7fffffff){
            ans+=l;
            while(path.size()){
                int e=path.top();
                path.pop();
                edge[e].w-=l;
                edge[e^1].w+=l; 
            }
        }
        else{
            break;
        }
        //printf("ans=%d\n",ans);
    }
    printf("%d\n",ans);
}
int main(){
    //freopen("P3931_2.in","r",stdin);
    cin>>n>>r;
    for(int i=1;i<n;i++){
        int x,y,w;
        cin>>x>>y>>w;
        add(x,y,w);
        add(y,x,w);
    }
    dfs(r);
    maxflow();
    return 0;
}

这个数据量 $\text{10w}$ 都能过为啥能过呢，据评论区大佬说，因为树是二分图，因此增广路不会超过 $log_2n$ 条，因此这题我这么写能过，但是遇到非树的毒瘤图那真的 $200$ 都能卡住的，而且我下了一下标板的测试点，貌似就是会陷入死循环，我不知道哪里写出来的问题了。

EK算法

在高中的时候我们老师就讲过，在一般情况下，$\text{dfs}$ 一定是没有 $\text{bfs}$ 优的。因此我们每次都挑一个看上去路径最短的增广路，既然要求最短了我们就可以用 $\text{bfs}$ 去寻找增广路了。

EK算法可以通过标板——P3376

我写的程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include<bits/stdc++.h>
#define int long long
#define maxn 500
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
struct eee{
    int to;
    int w;
    int next;
}edge[5005<<1];
struct ee{
    int v;
    int edge;
}pre[5005<<1];

int root[maxn],inque[maxn],cnt=1;
int n,m,s,t;
inline void add(int x,int y,int w){
    edge[++cnt]={y,w,root[x]};
    root[x]=cnt;
}
bool bfs(){
    queue<int>q;
    memset(inque,0,sizeof(inque));
    memset(pre,0xff,sizeof(pre));
    inque[s]=1;
    q.push(s);
    while(q.size()){
        int u=q.front();
        q.pop();
        for(int i=root[u];i;i=edge[i].next){
            int v=edge[i].to;
            if(!inque[v]&&edge[i].w){
                pre[v]={u,i};
                if(v==t){
                    return 1;
                } 
                inque[v]=1;
                q.push(v);
            }
        }
        
    }
    return 0;
}
void EK(){
    long long ans=0;
    //printf("%lld\n",sizeof(ans));
    while(bfs()){
        long long mi=inf;
        for(int i=t;i!=s;i=pre[i].v){
            mi=min(mi,edge[pre[i].edge].w);
        }
        for(int i=t;i!=s;i=pre[i].v){
            edge[pre[i].edge].w-=mi;
            edge[pre[i].edge^1].w+=mi;
        }
        ans+=mi;
        
    }
    printf("%lld\n",ans);
}

void sync(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
}

signed main(){
    //freopen("P3376_7.in","r",stdin);
    sync();
    cin>>n>>m>>s>>t;
    while(m--){
        int x,y,w;
        cin>>x>>y>>w;
        add(x,y,w);
        add(y,x,0);
    }
    EK();
    return 0;
}

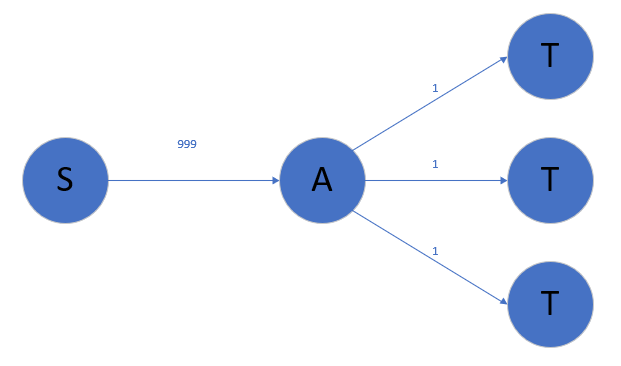
Dinic算法

EK算法虽然比较优了，但是有一个情况还是比较费时的，如下图所示

假设我 $S\to A$ 再经过更多的点，$A$ 后面的分支更多，那么每一次都要 $\text{bfs}$ 开销也是很大的的，重要的是很多路我们会重复遍历。这里就体现出了 $\text{Dinic}$ 算法的优了。

它只需要开始一次 $\text{bfs}$ 就能处理多条路径，它的思想是这样的：先对网络进行 $\text{bfs}$ 分层，我只找这样的增广路：

对于路径上任意 $u\to v$ 的边，都有 $v$ 在 $u$ 的下一层。我一次可以处理多条增广路，如果没有增广路那么我将对网络重新分层，直到 $\text{bfs}$ 无法遍历到汇点时。

标程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<bits/stdc++.h>
#define int long long
#define maxn 505
#define maxe 5005
using namespace std;
struct eee{
    int to;
    int w;
    int next;
}edge[maxe<<2];
int root[maxn],dep[maxn],cnt=1,s,t,n,m,ans;
queue<int>q;
inline void add(int x,int y,int w){
    edge[++cnt]={y,w,root[x]};
    root[x]=cnt;
} 
//网络分层 
bool bfs(){
    //puts("1");
    while(q.size())q.pop();
    q.push(s);
    memset(dep,0,sizeof(dep));
    dep[s]=1;
    while(q.size()){
        int u=q.front();
        q.pop();
        for(int i=root[u];i;i=edge[i].next){
            int v=edge[i].to,w=edge[i].w;
            if(!dep[v]&&w){
                dep[v]=dep[u]+1;
                q.push(v);
                
            }
        }    
    }
    return dep[t];
}
//从u出发，目前已有in的流量 
int dfs(int u,int in){
    if(u==t)return in;
    int ans=0;
    for(int i=root[u];i;i=edge[i].next){
        int v=edge[i].to,w=edge[i].w;
        if(dep[v]==dep[u]+1&&w){
            int res=dfs(v,min(in,w));
            edge[i].w-=res;
            edge[i^1].w+=res;
            in-=res;
            ans+=res;
        }
        
    }
    if(ans==0)dep[u]=0;
    return ans;    
}

void sync(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
}

signed main(){
    sync();
    cin>>n>>m>>s>>t;
    while(m--){
        int x,y,w;
        cin>>x>>y>>w;
        add(x,y,w);
        add(y,x,0);
    }
    int ans=0;
    while(bfs()){
        ans+=dfs(s,0x7fffffffffffffff);
    }
    cout<<ans<<endl;
}

又一个板子收入囊中，网络流应该会 $\text{Dcini}$ 差不多了吧qwq。