今天来复盘一下上次省赛考到的题目，异常地折磨人。

先说一下这题比赛的情况吧，基本上呢，银奖中等偏上的队伍都是做出来了的。

那我们就看看这题吧。

题目简介

什么思路在题目名字这里就一目了然了，那自然是最短路径。

而当我一眼扫过去看到这个数据量的时候瞬间惊呆。\(1≤n≤100000，1≤m≤200000\)，不仅如此，还有 \(q\) 次询问最短路径，\(q≤200000\) 当时一看，这玩你妈。给一个点都勉强能过了，这有这么多点，如果按照常规思路，一次单源最短路径复杂度 \(nlog_2n\) 然后 \(q\) 次询问，总复杂度就是 \(qnlog_2n\) 全部以最大值带进去妥妥的超时。所以当时比赛的时候看到这个题目是直接放弃了的，而且英文不好的我留下了悔恨的眼泪。

题目分析

但是它还有一个条件，那就是，直接相连的两个点当中，其中一个点的编号一定是另一个点的二进制前缀，这就说明了一点，\(2\) 它一定不会跟 \(3,6,12……\) 等点连接起来的，因为它们的前缀是 \(11_{2}\)，而 \(2_{10}\) 是 \(10_{2}\) 开头的，那么这样的话我们就可以构造一棵 \(tire\) 树。像这样子。

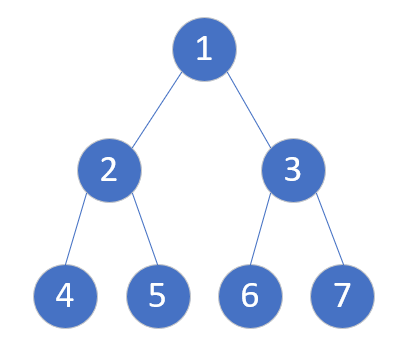
可以很明显的看出来是一个完全二叉树，这里我们假设往左子树走二进制右添一个 \(0\)，向左走二进制右添一个 \(1\)。那你可能会想，这明明边的范围是比点多的，怎么可能是一棵树。没错，但是我们看看，它能不能边横向添加？答案当然是否定的，因为一个得是另一个的前缀，同层次的话二进制位数相同，但是实际值不同，因此不可能满足这个条件。那么我们看看能不能连到其它不是我的祖先的节点呢？答案当然还是否定的，因为我简历的 \(tire\) 就是根据二进制后面添 \(0\) 还是添 \(1\) 来确定分支的，如果你都不是由我在后面添 \(0\) 或者是添 \(1\) 得到的那你就不可能是我的前缀，也不是我的孙子节点。

当然在图中 \(1\) 和 \(4\) 是可以直接相连的，虽然越级但是满足条件。所以它严格意义上来说不是树，但它怎么当成树呢？如果我把一个节点两个直接相连的子图当成子树，问题就解决了。因为两个子图之间肯定没有线连接，这个在刚刚已经证明过了。

对于每一个节点，我们都去寻找它祖先的最短路径。因为一个节点最多有 \(log_2n\) 个祖先，所以跑一下最短路算法问题还是不大的。我们定义 \(dis[i][k]\) 为节点 \(i\) 到达往上 \(k\) 个祖先的最短路径。那么对于任意两点的最短路径，我只需要寻找它们的最近公共祖先，然后答案就是 \(a\) 到最近公共祖先的最短路加上 \(b\) 到最近公共祖先的最短路。当然我们还有一个情况得考虑，因为 \(dis[i][k]\) 的定义仅仅是到它祖先的最短路径，而不是到这个节点的最短路径。因此它祖先的祖先可能有更优的路线。

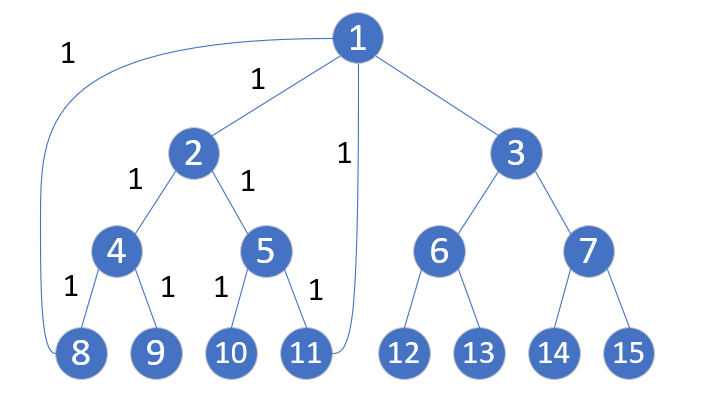
就比如这样一个图，图中我把关键数据标注出来了，无关数据没有标注。

如果说我要求 \(8\) 和 \(11\) 的最短路，按照我刚刚的定义很容易算的出来，它们的 \(LCA\) 是 \(2\)，然后 \(8\) 和 \(11\) 到 \(2\) 的最短路径都是 \(2\)，所以我算出来 \(8\) 到 \(11\) 的最短路径是 \(4\)，但是显然这里还有一个更优的解，那就是 \(8\to1\to11\) 这样才只有 \(2\) 的距离。但是最优的路线只可能存在于它的祖先上面了，其它地方不可能有。因此我们在用刚刚那个算法的时候还得兼顾一下查找 \(LCA\) 的祖先的答案。

这样子的话，假如我们能在规定时间内预处理完数据，那么我们每次查询的时间复杂度就只有 \(O(log_2n)\) 了，也不会超时。那么我们看看怎么去预处理这个 \(dis\) 数组。

我们只需要以每一个节点为根节点，和根节点的子节点作为一张图去跑单源最短路即可。对于 \(1\) 来说，它的复杂度会是 \(O(nlog_2n)\) ，每向下走一层，根节点数量翻倍，子节点数量减半。第二层中，总共复杂度将是 \(O(2 \times \frac{n}{2}log_2\frac{n}{2})\) 这么算下来这一层接近 \(O(nlog_2n)\) ，此后每一层都接近 \(O(nlog_2n)\)。它一共有几层呢？\(log_2n\)层。所以预处理的时间复杂度仅仅只有 \(O(n(log_2n)^2)\) 这个时间复杂度是完全不会超时的。

我们肯定还是选择 \(dijsktra\) 算法作为我们的单源最短路算法，加上一个优先队列优化，单源最短路需要每一个点给一个 \(d\) 数组标记所有节点到源点的最短路，但是这样空间会炸。所以我们每次跑最短路空间得共用，如何保证他们不会串呢？用标记数组。比如我在以 \(1\) 为根节点的时候，我就给标记打上 \(1\)，当我要更新 \(d\) 里面的值的时候我先比较一下上一个使用 \(d\) 数组的时候这个标记是否为我当前的根节点，如果是则更新，如果不是，则先初始化为一个很大的值。一般情况下我们选择 \(INF=0x3f3f3f3f3f3f3f3f\) 因为这样不容易溢出，也能表示无穷大。

但是呢，想想 \(dijsktra\) 算法还有什么需要注意的？那就是每次选完一个点的时候，它不会再被更新，这个时候我需要再打上一个标记，防止它被其它相连的边重复更新答案。一般情况下我们是选择 \(0,1\) 的，但是这里我们要一起用我们就选择根节点的值呗，如果当前根节点和这个值不相等说明这个点没有被添加，那就添加并将标记更新为当前的根节点。

那么思路清晰了我们就开写。

循序渐进

首先开这么几个数组

  • \(d[i]\) 表示 \(i\) 点到当前根节点的最短路径
  • \(vis1[i]\) 表示 \(i\) 节点上一次被 \(vis1[i]\) 节点标记为已经添加最短路的答案
  • \(vis2[i]\) 表示 \(i\) 节点的 \(d[i]\) 上一次是在以 \(vis2[i]\) 为根节点时更新的

图的话我们采用经典链式前向星存储，优先队列我们存储这么两个信息：

  1. x节点的最短路径
  2. x节点

我们肯定每次是以最路径为关键字进行小根堆构造的，这样保证每次 \(pop\) 出来的答案都是当前未被添加的节点中最小的那个答案。

于是我们不难写出以下代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void dijkstra(int root){
    p.push({0,root});//先把根节点丢进去
    d[root]=0;//自己到自己肯定就是0
    vis2[root]=root;//自己这个答案肯定要被标记，防止下面找到被初始化，当然你如果严格规定所得节点必须<root也没关系，因为下面会被初始化为INF。
    while(!p.empty()){
        auto x=p.top();
        p.pop();
        int point=x.second;//当前找到了一个距离最短的节点
        if(vis1[point]==root)continue;//如果已经被添加过了那么就不做以下处理
        vis1[point]=root;//把这个节点标记为已经添加进了答案中
        dis[point][cal_c(point,root)]=d[point];//更新答案，这里的cal_c用于判断root在point的第几个祖先，我们设父亲为第一个祖先。
        for(int i=head[point];i;i=edge[i].next){//更新所有与之相连的点的答案
            int to=edge[i].to;
            if(to<root)continue;//基本判断防止找到root的父亲
            if(vis2[to]!=root){//如果不是root说明上一次使用d[to]数组的还是上一次……啊不，是没用过d[to]这个值，所以要被初始化为一个无穷大
                d[to]=INF;
                vis2[to]=root;//标记
            } 
            if(d[point]+edge[i].w<d[to]){//单源最短路判断
                d[to]=d[point]+edge[i].w;
                p.push({d[to],to});//push进优先队列中
            }
        }
    }
}

那么结合代码中你的注释相信你已经不难理解这个 \(dijsktra\) 算法了。

我们再看看查询这部分的代码应该怎么写，无非就是先求出 \(LCA\) ，然后循环 \(LCA\) 以及 \(LCA\) 祖先的答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
while(q--){
    int x,y;
    cin>>x>>y;
    int lca=LCA(x,y);//先求最近公共祖先
    int lx=cal_c(x,lca),ly=cal_c(y,lca);//算出他们在那个点的第几个祖先
    int ans=INF;
    while(lca){
        ans=min(ans,dis[x][lx]+dis[y][ly]);//寻找最小值
        lx++,ly++;//每次往上看看那个祖先
        lca>>=1;//完全二叉树怎么找自己的父亲，这个不难吧？
    }
    if(ans==INF)printf("-1\n");
    else printf("%lld\n",ans);//输出答案
}

重要的部分写完了之后那么整个程序就呼之欲出了，但是一定得注意，不开 \(long long\) 见祖宗哦。

然后还有一点就是，既然你开了 \(long long\) 一定不要忘了 \(inf\) ，不要漏写一半，不然真到比赛要么哭罚时，要么哭整整一题了，不管前者后者，都是很伤的，建议先记在心里。

标程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include<bits/stdc++.h>
#define maxn 100005
#define INF 0x3f3f3f3f3f3f3f3f
#define int long long
using namespace std;
typedef pair<int,int> P;
struct eee{
    int next;
    int to;
    int w;
}edge[maxn<<2];
int head[maxn],dis[maxn][30],cnt,n,m;
int vis1[maxn];
int vis2[maxn];
int d[maxn];
priority_queue<P,vector<P>,greater<P> > p;
int cal_c(int child,int ancestor){
    int cnt=0;
    while(child>ancestor){
        cnt++;
        child>>=1;
    }
    return cnt;
}

void add(int x,int y,int w){
    edge[++cnt].next=head[x];
    edge[cnt].to=y;
    edge[cnt].w=w;
    head[x]=cnt;
} 

void dijkstra(int root){
    p.push({0,root});
    d[root]=0;
    vis2[root]=root;
    while(!p.empty()){
        auto x=p.top();
        p.pop();
        int point=x.second;
        if(vis1[point]==root)continue;
        vis1[point]=root;
        dis[point][cal_c(point,root)]=d[point];
        for(int i=head[point];i;i=edge[i].next){
            int to=edge[i].to;
            if(to<root)continue;
            
            if(vis2[to]!=root){
                d[to]=INF;
                vis2[to]=root;
            } 
            if(d[point]+edge[i].w<d[to]){
                d[to]=d[point]+edge[i].w;
                p.push({d[to],to});
            }
        }
    }
}
int LCA(int a,int b){
    while(a!=b){
        if(a>b)a>>=1;
        else b>>=1;
    }
    return a;
}

signed main(){
    //freopen("1.in","r",stdin);
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y,w;
        cin>>x>>y>>w;
        add(x,y,w);
        add(y,x,w);
    }
    
    memset(dis,0x3f,sizeof(dis)); 
    for(int i=1;i<=n;i++){
        dijkstra(i);
    }
    int q;
    cin>>q;
    while(q--){
        int x,y;
        cin>>x>>y;
        int lca=LCA(x,y);
        int lx=cal_c(x,lca),ly=cal_c(y,lca);
        int ans=INF;
        while(lca){
            ans=min(ans,dis[x][lx]+dis[y][ly]);
            lx++,ly++;
            lca>>=1;
        }
        if(ans==INF)printf("-1\n");
        else printf("%lld\n",ans);
    }
    return 0;
}

蒟蒻的提交记录。

测评网站

至于踩的那几个坑嘛，就是 \(long long\) 的问题了，然后还有一点就是输入的问题，这个具体看我上一篇博客吧，我到现在还没太弄懂，不过至少能注意规避的技巧了：那就是千万别在开

1
ios::sync_with_stdio(false);

的情况下用 \(scanf\) 去读取 \(long long\) 数据，不然你会怀疑人生。

希望这次省赛能超越上次的自己吧，\(xia0ji233,fighting！！！\)