洛谷P6037题解
浅谈基环树(环套树)
在题目开始之前,就唠一唠这个叫基环树的结构。准确来说,基环树它已经不是树了,我们知道,树一定是由 $n$ 点和 $n-1$ 条边组成的。而基环树是由 $n$ 点与 $n$ 边组成。但是因为它跟树还是很像,并且在保证连通的情况下有且仅有一个简单环,因此得名。如果不连通,那么它会成为基环树森林。
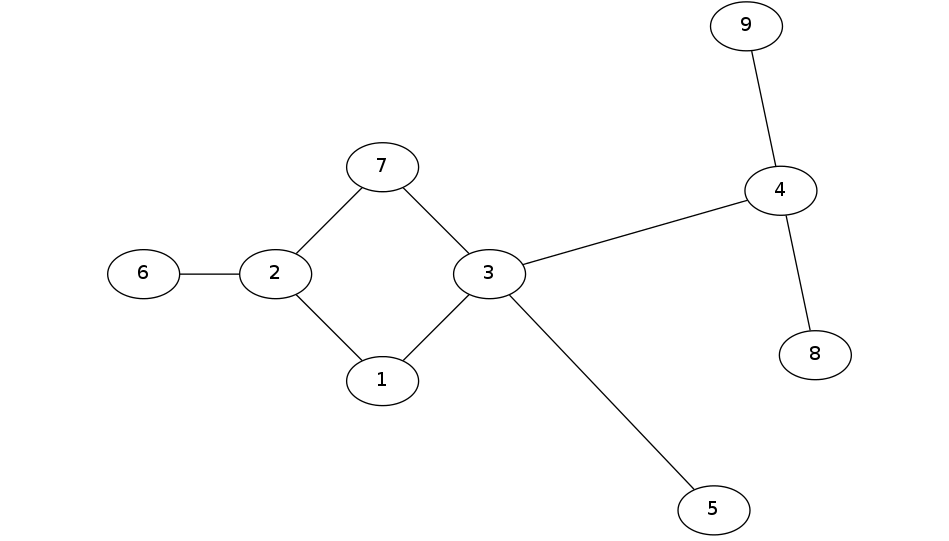
比如上图就是一个基环树。我们可以很清楚的看出来,点 $2,1,3,7$ 形成了环,断开任意一条属于环中的边都会使这个棵基环树成为树。一般情况下都是将环和环连接的子树进行分开讨论。如何求环呢?我们只需要 dfs 一遍就行了,如果遇到被访问过的点,那就依次返回路径上的所有点,直到我遇到的那个点为止。
举个例子,在上图中,我从 6 开始 dfs,假设它经历了 $6 \to 2 \to 1 \to 3 \to 7$ 的顺序。那么接下来在搜索 7 的时候就会发现与它相连的点 2 已经被访问过,那么我返回值给个 2,依次回溯,回溯过程中将点入栈或者入一个 $vector$ 都可以。直到回溯到 2 这个点为止。环就被我们求出来了。
能求出环我们就会很好做这类的题目了,那么我们具体看看这题吧。
题目描述
Ryoku 所处的世界可以抽象成一个有 n 个点, n条边的带权无向连通图 G。每条边有美观度和长度。
Ryoku 会使用这样一个策略探索世界:在每个点寻找一个端点她未走过的边中美观度最高的走,如果没有边走,就沿着她前往这个点的边返回,类似于图的深度优先遍历。
探索的一个方案的长度是这个方案所经过的所有边长度的和(返回时经过的长度不用计算)。
她想知道,对于每一个起点 $s=1,2,\cdots,n$,她需要走过的长度是多少?
$n$ 个点 $n$ 条边的连通图,那么肯定就是基环树了然后它会根据美观度与深度优先的一种搜索策略,即遇到分支先沿一条分支走完再走另一条分支,并且多条分支优先搜索美观度高的分支。回溯走的路不算,问你以不同的点为起点搜索完所有的点需要走多少长度。
我们不难得出,如果要遍历 $n$ 个点,我们只需要走过 $n-1$ 条边。而对于一棵树而言,对它深度优先搜索一定会遍历树上所有的边。因此如果把基环树拆开称为一个环和若干个子树,我们就只需要在环上讨论情况,子树的所有边一定是都会走过的。对于同一个环,我先向右边遍历和先向左边遍历走的路径是完全不一样的,如果先向右边那必然导致它左边不会被走过,同理先走左边那右边就不会被走过。
再根据题中的策略,对于环上的点,我们只需要循环一遍环上的所有点,观察与它连接的在环上的边的美观度哪个比较大,那么答案就是所有图的边权减去那个美观度较小的边权。对于不在环上的点我们可以观察它所在的子树连接在环的哪个点,因为从那个点遍历出来最终也会从它所在的子树走向环的那个点,然后情况就变成了在换上对应的点遍历的情况了。
所以我们先大致描述一下算法流程:
- 将边按照出点读入 $vector$ 当中,并且按美观度排序
- dfs 跑出环上的点将其标记
- 对环上所有的点进行答案计算
- 对环上的点再跑一次dfs,然后搜索策略为非环上的点,将搜索到的点标记为环上对应的那个点
- 最后答案就出来了
标程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| #include<bits/stdc++.h>
#define maxn 3000005
using namespace std;
struct eee{
int to;
int w;
int p;
};
int visited[maxn],ans[maxn],n;
long long sum_len,res[maxn];
vector<eee>edge[maxn];
vector<int>s;
bool in_stack[maxn];
void add(int x,int y,int w,int p){
eee e;
e.to=y;
e.w=w;
e.p=p;
edge[x].push_back(e);
}
int cmp(eee a,eee b){
return a.p>b.p;
}
int dfs(int u,int pre){
if(visited[u]){
return u;
}
visited[u]=1;
int value=0;
for(auto it=edge[u].begin();it!=edge[u].end();it++){
int v=it->to;
if(v==pre||in_stack[v])continue;
int tmp=dfs(v,u);
if(tmp){
value=tmp;
if(value==u){
value=0;
}
s.push_back(u);
in_stack[u]=1;
}
}
return value;
}
void dfs2(int u,int pre,int flag){
for(auto it=edge[u].begin();it!=edge[u].end();it++){
int v=it->to;
if(v==pre||in_stack[v])continue;
ans[v]=flag;
dfs2(v,u,flag);
}
}
int main(){
std::ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
int x,y,w,p;
cin>>x>>y>>w>>p;
add(x,y,w,p);
add(y,x,w,p);
sum_len+=w;
}
for(int i=1;i<=n;i++){
sort(edge[i].begin(),edge[i].end(),cmp);
}
dfs(1,0);
for(auto i=s.begin();i!=s.end();i++){
dfs2(*i,0,*i);
ans[*i]=*i;
}
for(auto i=s.begin();i!=s.end();i++){
for(auto j=edge[*i].end()-1;j!=edge[*i].begin()-1;j--){
if(in_stack[j->to]){
res[*i]=sum_len-(j->w);
break;
}
}
}
for(int i=1;i<=n;i++){
printf("%lld\n",res[ans[i]]);
}
return 0;
}
|
