然后今天来学二分图，首先我们来看看二分图的定义。

二分图的定义

首先二分图它是一个图(G)，由点集(V)和边集(E)构成的集合，即G=(V,E)。

除此之外它还满足一个特点，若这个图的点集存在一个划分{V1,V2}使得，任意的e(i,j,w)∈E满足关系，i∈V1,j∈V2或者是i∈V2,j∈V1。那么这个图就被称为一个二分图。

以上是比较数学的说法，而且是自己DIY的(狗头。那说人话就是说，如果你能找到一个合理的方式把点划成两个部分，使得每条边的两个顶点均不同时属于一个部分。那么它就是一个二分图。反之，如果不存在这样的划分满足以上结果，那么它就不是一个二分图。

二分图的一个等价定义是：不含有含奇数条边的环的图。

如果说了这么多让你感觉到还是有一点点难以理解的话，那么我们换一个思路：假设把人比作点，把相爱关系比作边。假设这个人群内没有舔狗(恋情非单向)和男酮，那么它们的关系组成的图就会是一个二分图。时间管理大师(一人同时与多人)不影响它还是一个二分图的，只要没有同就行。不知道这个例子是否够抽象，更易于理解。

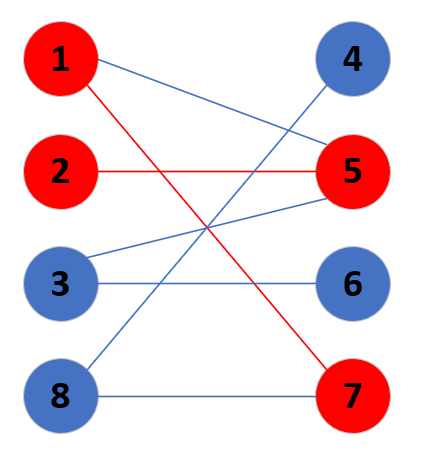
举个例子，如下图，它是不是一个二分图？

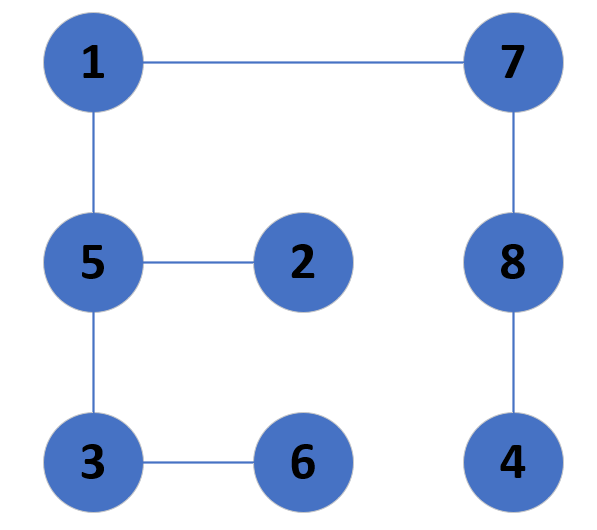
判断二分图可以用它的性质，显而易见的性质是什么：边连接的两个点一定属于不同集合。用刚刚那个例子再去讲的话就是：没有同的情况下，喜欢男孩的一定都是女孩，而这里我们划分就是以男孩女孩作为依据划分的，接着往下推又可以得到：喜欢喜欢男孩的人的人一定也是男孩。这里我们从1开始，假设1为男，那么5，7必为女，2，8，3必为男，6，4必为女。

我们就可以得到划分：{{1,2,3,8},{4,5,6,7}}。那么我们稍微画的明显一点，将两个划分独立为两排，得到了以下图。

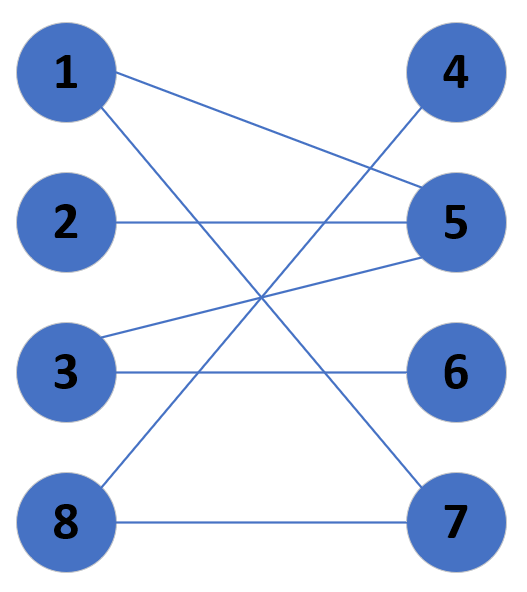
为了方便，我们一般都会把二分图化成这种形式，可以很清楚的发现，同一排之间的点没有连线。那么你现在一定对二分图有了一个较为清楚的认识，那么可能会疑惑，这样的数据结构能用来处理什么样的问题呢？那么就涉及到我们接下来讲的概念了。

一些概念

  1. 匹配(matching)：匹配其实就是一个边的集合，任意两条属于匹配的边都没有公共顶点，那么这个集合就叫做这个图的一个匹配。
  2. 匹配点：如果这个点存在于这个匹配的任意一条边上，那么这个点就是一个匹配点。
  3. 匹配边：如果这个边属于这个匹配，那么这就是一个匹配边。
  4. 非匹配点：与匹配点相对
  5. 非匹配边：与匹配边相对
  6. 最大匹配：在所有匹配中，所含边数量最多的称为最大匹配。
  7. 完美匹配：如果一个匹配中的所有边包含了一个图的所有点，即，一个图当中所有的点都为匹配点时，这个匹配称为完美匹配，并非所有的图都含有完美匹配，完美匹配一定是最大匹配。

实际应用

比如还是上面这个图，假设它们就是四男四女，我们要怎样做，才能尽可能保证它们都和自己喜欢的人凑成一对呢？这实际上就是要求二分图的最大匹配了，最大匹配我们一般是用匈牙利算法，对于匈牙利算法，我们需要再补充一点概念。

  1. 交替路：如果从一个非匹配点出发，依次经过匹配边，非匹配边，匹配边，非匹配边……形成的路径就叫交替路。
  2. 增广路：如果交替路的终点为一个非匹配点，那么这条交替路我们又叫增广路。

如下图

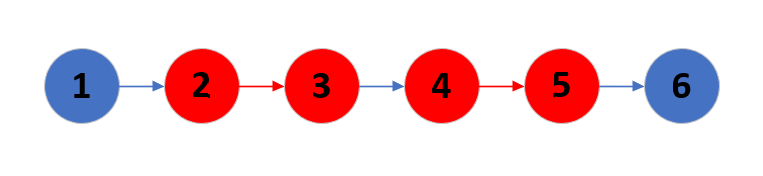
红色点和红色边为匹配点和匹配边，这是一条增广路。

增广路的性质就是非匹配边会比匹配边多一条。如果我们把匹配边和非匹配边交换顺序，那么将会得到

可以到相比之前多了一个匹配边和两个匹配点。但是匹配顺序完全不一样了，原来是2，3匹配，4，5匹配，现在2，3和4，5都不在同一条匹配边上。

匈牙利算法的本质就是不停寻找增广路，增加匹配数目的。我们先不考虑匈牙利算法的代码，先徒手做一遍。首先我们需要匹配的点只有一边，另一边是被匹配的。

如最开始那个图，

从1开始，遍历边，先看1，5，发现5未被匹配，则直接匹配，结束。

那么现在的图是这样的。

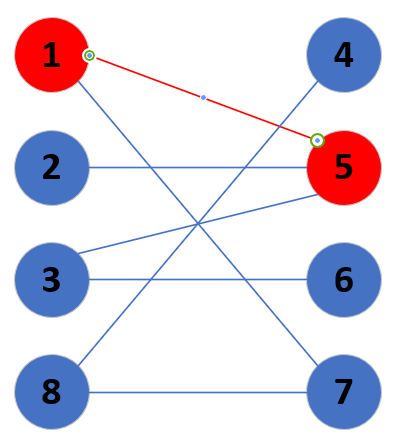
从2开始，2未被匹配，则寻找与它相连的边，找到(2,5)，但是发现5已经被匹配了，这个时候就要用到寻找增广路的思维了。那么我们直接沿着匹配边搜寻，就找到了1，然后从1开始找相连的边，因为不能反复横跳，所以我们只能选择7，发现7没被匹配，因此2-5-1-7构成增广路，找到增广路之后代表首位两个点参与进了匹配。然后交换匹配边与非匹配边。成了这样

这里我们不考虑最好的情况，因为我们自己很清楚3，6匹配，4，8匹配直接就完结撒花了。但是计算机不一定按照这样的方式去遍历，你要保证先后顺序不影响最终结果，即就算你选择5，最终算出来的最大匹配应当也是4。

这里我们选5，发现5被匹配了，于是找到2，但是2之后再也找不到路径了，因此(3,5)方向上的增广路寻找失败，所以就会找(3,6)，(3,6)直接匹配，我们看看最后这个8会怎么样呢，我们假设也是先找到了7，7会找到1，1会找到5，5找到2，发现2找不到增广路了，返回失败。所以最终选择了(8,4)。那么这样一整个就是匈牙利算法了。

这里用C代码大概写一下，假设存图采用链式前向星。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>
using namespace std;
struct eee{
    int to;
    int next;
}edge[MAX_EDGE];
int match[MAX_NODE],check[MAX_NODE],root[MAX_NODE];
vector<int>s;//存储一边的点集
void add(int x,int y){
    edge[++cnt].to=y;
    edge[cnt].next=root[x];
    root[x]=cnt;
}
int dfs(int u){
    for(int i=root[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(!check[v]){
            check[v]=true;
            if(match[v]==-1||dfs(match[v])){
                match[u]=v;
                match[v]=u;
                check[v]=false; 
                return true; 
            }
        }
    }
    return false;
}
int xyl(){
    int ans=0;
    for(int i=0;i<s.size();i++){
        if(match[s[i]]==-1){
            check[s[i]]=true;
            if(dfs(s[i]))ans++;
            
        }

    }
    return ans;
}

例题

洛谷P1129

小 Q 是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个 n \times nn×n 黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：

  • 行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）。
  • 列交换操作：选择矩阵的任意两列，交换这两列（即交换对应格子的颜色）。

游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。

对于某些关卡，小 Q 百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！于是小 Q 决定写一个程序来判断这些关卡是否有解。

题意简单明了就是给一个01矩阵，问你能不能通过行交换与列交换将主对角线的元素都变成1。

那么其实就是每一行找到一个1，使得每个1处于不同的列。只要找到，那么经过若干次交换一定能使主对角线元素都为1。如果第一行的第三列存在一个1，那么就让1和3相连。当然因为这里的3不能和第三行混淆，所以我们选择列数+n作为二分图的另一个点集。所以我们只需要让行列都匹配那就完成了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
struct eee{
    int to;
    int next;
}edge[100000];
int cnt,n,root[501],check[500],match[500];
void add(int x,int y){
    //printf("%d %d\n",x,y);
    edge[++cnt].to=y;
    edge[cnt].next=root[x];
    root[x]=cnt;
}
int dfs(int u){
    for(int i=root[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(!check[v]){
            check[v]=true;
            if(match[v]==-1||dfs(match[v])){
                match[u]=v;
                match[v]=u;
                check[v]=false; 
                return true; 
            }
        }
    }
    return false;
}
int xyl(){
    int ans=0;
    for(int i=1;i<=n;i++){
        if(match[i]==-1){
            check[i]=true;
            if(dfs(i))ans++;
            
        }

    }
    return ans;
}
void solve(){
    cin>>n;
    memset(root,0,sizeof(root));
    for(int i=1;i<=2*n;i++)match[i]=-1;
    cnt=0;
    string s;
    getchar();
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            int x;
            cin>>x;
            if(x==1){
                add(i,j+n);
                add(j+n,i);
            }
        }
    }
    if(xyl()==n){
        printf("Yes\n");
    }
    else{
        printf("No\n");
    }
}
int main(){
    //freopen("1.in","r",stdin);
    int t;
    cin>>t;
    while(t--)solve();
    return 0;
}

这里被卡了有点久，最后发现是数组越界，在使用前向星存无向图的时候一定要记得开两倍内存，不然写越界了很难说错误在哪。

血淋淋的教训，并且失败的俩测试点没有报错re，而是wrong answer。