AES加密学习
今天来学学AES。
AES简介
高级加密标准(AES,Advanced Encryption Standard)为最常见的对称加密算法(微信小程序加密传输就是用这个加密算法的)。对称加密算法也就是加密和解密用相同的密钥,具体的加密流程如下图:
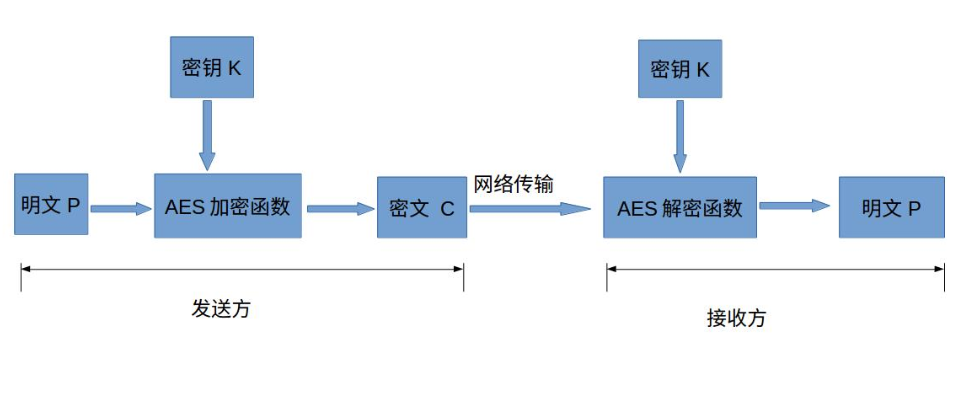
分组问题
AES属于分组加密,什么是分组加密呢,顾名思义,分组加密=分组+加密(狗头。分组就是说把它分成一个个组进行加密,可以把它和base64作为一个对比,base64是三个字符一组进行编码,那么既然是要分组那必然也会遇到分组不满的情况,这个时候需要加上填充。这个填充呢,有很多种方案。
零字节填充
这个可以说是比较常见的手段了,一般人一般也都能想得到,但是这样的话难以区分末尾的0到底是它的信息本来就存在的还是填充的,信息表达不明确。
填充n位n
这个略有点意思。但是假如它本来信息就有n位n呢?那么最后的那n位n还是没办法区分是不是它本来就有的。
那么最终AES采取了哪种填充方式呢?它选择在第二种方案中改进,如果长度刚好不需要填充,那么就填充16位16。这么一来,如果它末尾存在了n位n,但是由于长度满足16的倍数,那么还会填充16位16,这样它就能够区分填充位和明文位了。
AES常见分类
AES有三种常见加密标准,根据密钥位数不同用于区分,密钥的长度不同,推荐加密轮数也不同,如下表所示:
| AES | 密钥长度(字节) | 分组长度(字节) | 加密轮数 |
|---|---|---|---|
| AES-128 | 16 | 16 | 10 |
| AES-192 | 24 | 16 | 12 |
| AES-256 | 32 | 16 | 14 |
AES还有五种加密模式:1.电码本模式(Electronic Codebook Book (ECB));2.密码分组链接模式(Cipher Block Chaining (CBC));3.计算器模式(Counter (CTR));4.密码反馈模式(Cipher FeedBack (CFB));5.输出反馈模式(Output FeedBack (OFB))。
本片博客只介绍前两种模式。
AES加密流程
AES的EBC模式大概可以用下面的流程图图表示
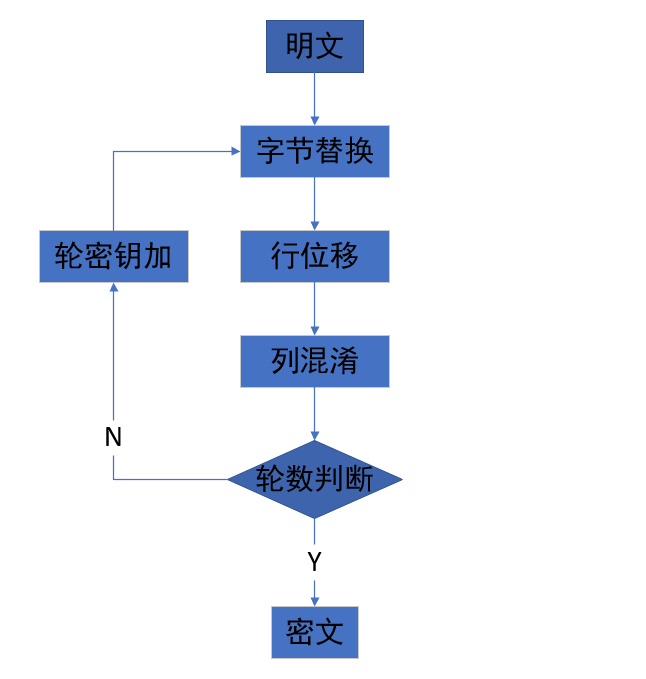
字节替换
官方的解释是,建立16*16的字节表,然后把自己拆成高4位和低四位,高四位位行,第四位为列好去查表替换。这个很好理解,其实就是在0x00-0xff字节内建立双射,让每个字节替换为其它字节。比如最简单的,我让所有字节都加1%256,也是一个双射变换。那么既然是一个双射,那么我们很容易求出它的逆。
一般AES加密用以下的字节替换表
| 行/列 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0x63 | 0x7c | 0x77 | 0x7b | 0xf2 | 0x6b | 0x6f | 0xc5 | 0x30 | 0x01 | 0x67 | 0x2b | 0xfe | 0xd7 | 0xab | 0x76 |
| 1 | 0xca | 0x82 | 0xc9 | 0x7d | 0xfa | 0x59 | 0x47 | 0xf0 | 0xad | 0xd4 | 0xa2 | 0xaf | 0x9c | 0xa4 | 0x72 | 0xc0 |
| 2 | 0xb7 | 0xfd | 0x93 | 0x26 | 0x36 | 0x3f | 0xf7 | 0xcc | 0x34 | 0xa5 | 0xe5 | 0xf1 | 0x71 | 0xd8 | 0x31 | 0x15 |
| 3 | 0x04 | 0xc7 | 0x23 | 0xc3 | 0x18 | 0x96 | 0x05 | 0x9a | 0x07 | 0x12 | 0x80 | 0xe2 | 0xeb | 0x27 | 0xb2 | 0x75 |
| 4 | 0x09 | 0x83 | 0x2c | 0x1a | 0x1b | 0x6e | 0x5a | 0xa0 | 0x52 | 0x3b | 0xd6 | 0xb3 | 0x29 | 0xe3 | 0x2f | 0x84 |
| 5 | 0x53 | 0xd1 | 0x00 | 0xed | 0x20 | 0xfc | 0xb1 | 0x5b | 0x6a | 0xcb | 0xbe | 0x39 | 0x4a | 0x4c | 0x58 | 0xcf |
| 6 | 0xd0 | 0xef | 0xaa | 0xfb | 0x43 | 0x4d | 0x33 | 0x85 | 0x45 | 0xf9 | 0x02 | 0x7f | 0x50 | 0x3c | 0x9f | 0xa8 |
| 7 | 0x51 | 0xa3 | 0x40 | 0x8f | 0x92 | 0x9d | 0x38 | 0xf5 | 0xbc | 0xb6 | 0xda | 0x21 | 0x10 | 0xff | 0xf3 | 0xd2 |
| 8 | 0xcd | 0x0c | 0x13 | 0xec | 0x5f | 0x97 | 0x44 | 0x17 | 0xc4 | 0xa7 | 0x7e | 0x3d | 0x64 | 0x5d | 0x19 | 0x73 |
| 9 | 0x60 | 0x81 | 0x4f | 0xdc | 0x22 | 0x2a | 0x90 | 0x88 | 0x46 | 0xee | 0xb8 | 0x14 | 0xde | 0x5e | 0x0b | 0xdb |
| A | 0xe0 | 0x32 | 0x3a | 0x0a | 0x49 | 0x06 | 0x24 | 0x5c | 0xc2 | 0xd3 | 0xac | 0x62 | 0x91 | 0x95 | 0xe4 | 0x79 |
| B | 0xe7 | 0xc8 | 0x37 | 0x6d | 0x8d | 0xd5 | 0x4e | 0xa9 | 0x6c | 0x56 | 0xf4 | 0xea | 0x65 | 0x7a | 0xae | 0x08 |
| C | 0xba | 0x78 | 0x25 | 0x2e | 0x1c | 0xa6 | 0xb4 | 0xc6 | 0xe8 | 0xdd | 0x74 | 0x1f | 0x4b | 0xbd | 0x8b | 0x8a |
| D | 0x70 | 0x3e | 0xb5 | 0x66 | 0x48 | 0x03 | 0xf6 | 0x0e | 0x61 | 0x35 | 0x57 | 0xb9 | 0x86 | 0xc1 | 0x1d | 0x9e |
| E | 0xe1 | 0xf8 | 0x98 | 0x11 | 0x69 | 0xd9 | 0x8e | 0x94 | 0x9b | 0x1e | 0x87 | 0xe9 | 0xce | 0x55 | 0x28 | 0xdf |
| F | 0x8c | 0xa1 | 0x89 | 0x0d | 0xbf | 0xe6 | 0x42 | 0x68 | 0x41 | 0x99 | 0x2d | 0x0f | 0xb0 | 0x54 | 0xbb | 0x16 |
那么它的逆表就是
| 行/列 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0x52 | 0x09 | 0x6a | 0xd5 | 0x30 | 0x36 | 0xa5 | 0x38 | 0xbf | 0x40 | 0xa3 | 0x9e | 0x81 | 0xf3 | 0xd7 | 0xfb |
| 1 | 0x7c | 0xe3 | 0x39 | 0x82 | 0x9b | 0x2f | 0xff | 0x87 | 0x34 | 0x8e | 0x43 | 0x44 | 0xc4 | 0xde | 0xe9 | 0xcb |
| 2 | 0x54 | 0x7b | 0x94 | 0x32 | 0xa6 | 0xc2 | 0x23 | 0x3d | 0xee | 0x4c | 0x95 | 0x0b | 0x42 | 0xfa | 0xc3 | 0x4e |
| 3 | 0x08 | 0x2e | 0xa1 | 0x66 | 0x28 | 0xd9 | 0x24 | 0xb2 | 0x76 | 0x5b | 0xa2 | 0x49 | 0x6d | 0x8b | 0xd1 | 0x25 |
| 4 | 0x72 | 0xf8 | 0xf6 | 0x64 | 0x86 | 0x68 | 0x98 | 0x16 | 0xd4 | 0xa4 | 0x5c | 0xcc | 0x5d | 0x65 | 0xb6 | 0x92 |
| 5 | 0x6c | 0x70 | 0x48 | 0x50 | 0xfd | 0xed | 0xb9 | 0xda | 0x5e | 0x15 | 0x46 | 0x57 | 0xa7 | 0x8d | 0x9d | 0x84 |
| 6 | 0x90 | 0xd8 | 0xab | 0x00 | 0x8c | 0xbc | 0xd3 | 0x0a | 0xf7 | 0xe4 | 0x58 | 0x05 | 0xb8 | 0xb3 | 0x45 | 0x06 |
| 7 | 0xd0 | 0x2c | 0x1e | 0x8f | 0xca | 0x3f | 0x0f | 0x02 | 0xc1 | 0xaf | 0xbd | 0x03 | 0x01 | 0x13 | 0x8a | 0x6b |
| 8 | 0x3a | 0x91 | 0x11 | 0x41 | 0x4f | 0x67 | 0xdc | 0xea | 0x97 | 0xf2 | 0xcf | 0xce | 0xf0 | 0xb4 | 0xe6 | 0x73 |
| 9 | 0x96 | 0xac | 0x74 | 0x22 | 0xe7 | 0xad | 0x35 | 0x85 | 0xe2 | 0xf9 | 0x37 | 0xe8 | 0x1c | 0x75 | 0xdf | 0x6e |
| A | 0x47 | 0xf1 | 0x1a | 0x71 | 0x1d | 0x29 | 0xc5 | 0x89 | 0x6f | 0xb7 | 0x62 | 0x0e | 0xaa | 0x18 | 0xbe | 0x1b |
| B | 0xfc | 0x56 | 0x3e | 0x4b | 0xc6 | 0xd2 | 0x79 | 0x20 | 0x9a | 0xdb | 0xc0 | 0xfe | 0x78 | 0xcd | 0x5a | 0xf4 |
| C | 0x1f | 0xdd | 0xa8 | 0x33 | 0x88 | 0x07 | 0xc7 | 0x31 | 0xb1 | 0x12 | 0x10 | 0x59 | 0x27 | 0x80 | 0xec | 0x5f |
| D | 0x60 | 0x51 | 0x7f | 0xa9 | 0x19 | 0xb5 | 0x4a | 0x0d | 0x2d | 0xe5 | 0x7a | 0x9f | 0x93 | 0xc9 | 0x9c | 0xef |
| E | 0xa0 | 0xe0 | 0x3b | 0x4d | 0xae | 0x2a | 0xf5 | 0xb0 | 0xc8 | 0xeb | 0xbb | 0x3c | 0x83 | 0x53 | 0x99 | 0x61 |
| F | 0x17 | 0x2b | 0x04 | 0x7e | 0xba | 0x77 | 0xd6 | 0x26 | 0xe1 | 0x69 | 0x14 | 0x63 | 0x55 | 0x21 | 0x0c | 0x7d |
比如在第一个表中可以看到0行0列是0x63,与之对应的,在第二张表的第6行第三列就是0x00,也就是0x63在第一个表中的位置。因为AES是对称加密,所以每一步操作都需要可逆。
行位移
这里要说一下,AES分组是16个字节一组,在加密的过程中16字节会形成4x4的矩阵,字节按照以下顺序排列
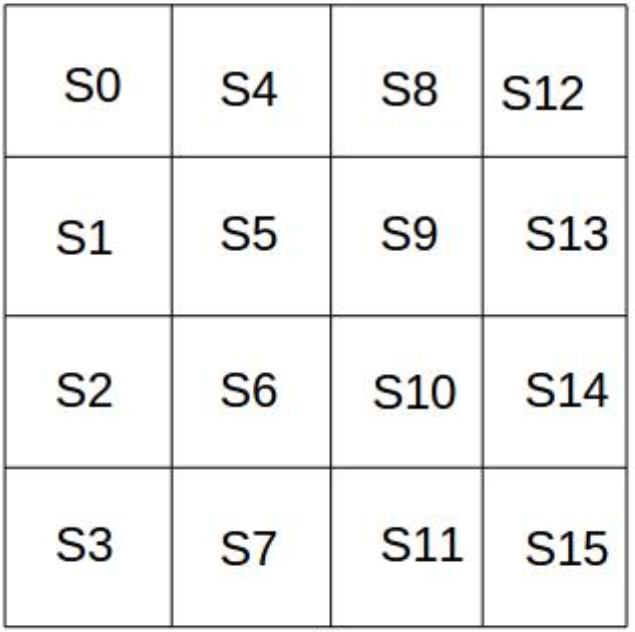
行移位是一个简单的左循环移位操作。第0行左移0字节,第1行左移1字节,第2行左移2字节,第3行左移3字节,如下图所示:
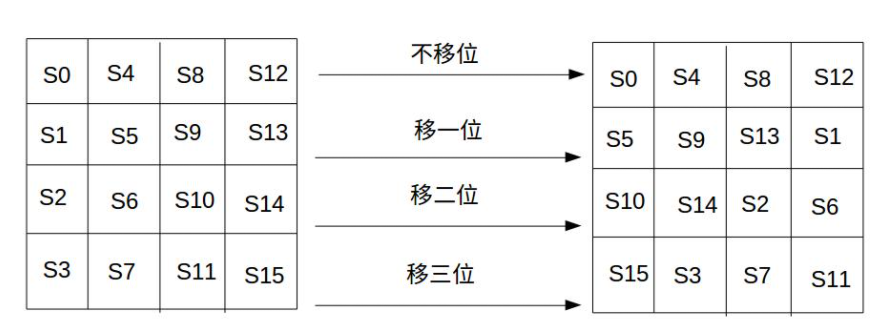
逆变换当然也很简单,就不细讲了。
列混淆
这个涉及到的知识比较多,我有点难以接受,mark一下,以后再补
就是说把它当成一个矩阵然后和另一个矩阵做乘法运算得到新的矩阵,至于逆过程就是对逆矩阵做乘法。然后这里面的加法就是异或,乘法会变成取模乘法。(应该是这样的)
轮密钥加
这个很简单,就是扩展密钥,密钥输入了16字节,每组四个字节就是四组,第一组和第四组异或得到第五组,第二组和第五组异或得到第六组,第三组和第六组异或得到第七组,以此类推。因为要加密10次,所以扩展出四十组密钥。
然后就是很简单的了,列混淆得到的矩阵再和密钥异或一下即可。每次都和不一样的密钥做异或,一共十次,这就是AES。
CBC模式
分组加密有一个缺点,分组之间独立,一样的数据不管在第几组都是一样的加密,如果我已只很多密文明文对,那么加密的信息很可能会被暴力破解出来,CBC就是用来对抗这个缺点的。CBC不通的就是,会有一个初始向量与第一组的数据进行异或,然后第二组的会和第一组异或加密前的数据异或再进行加密,以此类推,这样的话,分组之间将不再独立,改动前面的一个字节很可能导致整个密文发生巨大变化。