来快乐学算法了。
启发式搜索
启发式搜索(英文:heuristic search)是一种改进的搜索算法。它在普通搜索算法的基础上引入了启发式函数,该函数的作用是基于已有的信息对搜索的每一个分支选择都做估价,进而选择分支。简单来说,启发式搜索就是对取和不取都做分析,从中选取更优解或删去无效解。
在此之前,本蒟蒻一直就只会dfs和bfs,今天来学学新的搜索算法。经过多重资料的 查阅也是大概得知启发式搜索的大概思路,每次搜索会对之后可能的最优状态估值,如果估出来的值不如当前某些状态,那么我就直接舍弃这个状态。就比如经典01背包问题,我对每一个物品的抉择都有选或者不选两种选择,我发现我不选这个物品,选其它物品所产生的最优解不如我当前选这个解的状态好,那么我直接考虑选择这个而不去搜索不选择这个物品的状态。
估值函数
这里需要解释一下我如何判断当前状态是否优于之后的最优状态,那么这里需要这么一个估值函数,估值函数不是真的对那个情况做具体分析,那样的话跟暴力没区别了。我这样考虑,如果剩下所有物品全能放进去都不如我一个放进去价值大,那么我肯定得放这个物品(前提是放得进去,放不进去就别讨论了)。那么这个剩下的所有物品的价值就是我这一个启发式搜索方案的估值函数。
假如有n样物品,那么在搜索第x样物品的估值函数就是
$f(x)=\sum _{i=x} ^{n} a[i]$
我在判断一下这个要不要放的时候我只需要看看我历史最优值是否小于当前最优值+估值函数值就可以了,如果成立那就说明这个可能可以不放,否则这个必须要放,因为如果不放的话,它剩下就算全放都没有我历史搜索出来的最优值大,那么我就没必要搜索不放的情况了。当然这是其中一种启发式搜索的办法。还有其它的方式,我们下面讲。
例题分析
来自洛谷P1048 NOIP2005 普及组 采药
那么我按照我之前的启发式搜索方式得到了下面的算法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include<stdio.h>
#include<algorithm>
#define maxn 10001
int v[maxn],c[maxn];
int ans=0;
int n,m;
int f(int x){
int ans=0;
for(int i=x+1;i<=n;i++){
ans+=v[i];
}
return ans;
}
void search(int now,int contain,int value){
if(value>ans)ans=value;
if(now>n)return ;
if(contain>=c[now])
search(now+1,contain-c[now],value+v[now]);
if(f(now)+value>ans)
search(now+1,contain,value);
}
int main(){
scanf("%d %d",&m,&n);
for(int i=1;i<=n;i++){
scanf("%d %d",&c[i],&v[i]);
}
search(1,m,0);
printf("%d\n",ans);
return 0;
}
|
可以算出正确结果,但是有些点会T
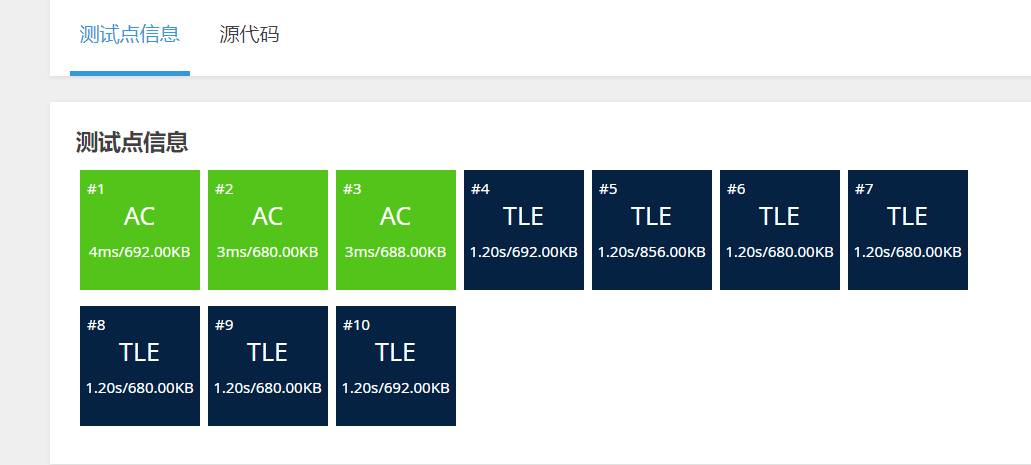
事实上我这样的启发式搜索方法还是有点暴力,因为后面的物品可能完全一个都放不进去,但是价值很大,这样的数据启发式搜索就会退化成朴素算法。
那么我如果换一种,我不管什么就一个个放进去看看能有多少最大的价值,为了保证能朴素地算出最大值我们可以先对物品的单位价值排序然后一个个放,而且我们需要假设物品可以分割。那不然的话等于是在后面的物品做一次动态规划,复杂度还是比较高的。所以我们可以得出估值函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
| int f(int x,int res){
int ans=0;
for(int i=x+1;i<=n;i++){
if(res>c[i]){
ans+=v[i];
res-=c[i];
}
else{
return ans+d[i]*res;
}
}
return ans;
}
|
然后写出以下的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include <algorithm>
#include <stdio.h>
#define maxn 10001
using namespace std;
struct item{
int c,v;
double d;
}a[maxn];
int ans=0;
int n,m;
int f(int x,int res){
int ans=0;
for(int i=x+1;i<=n;i++){
if(res>a[i].c){
ans+=a[i].v;
res-=a[i].c;
}
else{
return ans+(int)(a[i].d*res);
}
}
return ans;
}
void search(int now,int contain,int value){
if(value>ans)ans=value;
if(now>n)return ;
if(contain>=a[now].c)
search(now+1,contain-a[now].c,value+a[now].v);
if(f(now,contain)+value>ans)
search(now+1,contain,value);
}
bool operator<(const item &a, const item &b)
{
return a.d > b.d;
}
int main(){
scanf("%d %d",&m,&n);
for(int i=1;i<=n;i++){
scanf("%d %d",&a[i].c,&a[i].v);
a[i].d=(double)a[i].v/a[i].c;
}
sort(a+1,a+1+n);
search(1,m,0);
printf("%d\n",ans);
return 0;
}
|
成功AC。
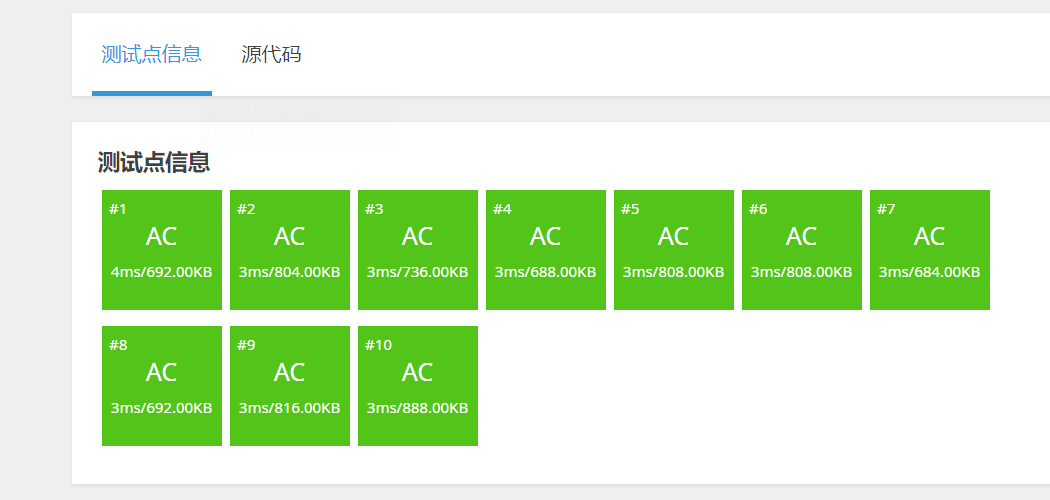
由此可见,只要我们选的估值函数够好,那么搜索它就不会那么暴力了,这大概也是启发式搜索算法的精髓,只要估值函数选的好,复杂度能直接从指数级降到(其实我也不知道是多少hhh),但是个人觉得,只要估值函数写出来了,都是没问题的,因为代码量本身就很少,只是在做决策之前估计以下这一步到底值不值得就好了,然后就是递归大法好,可以看到我的search函数本身就这几句。
那么在这样的搜索里面启发式算法的估值函数很容易求,但是如果是迷宫类的问题,启发式算法还真的就难说了,等明天去看看迷宫类的启发式搜索吧。

