RSA解密简介:RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的 。(from 百度百科)

非对称加密

我们平时学习的加密多是对称加密，非对称加密相比于对称加密的区别就是:加密和解密用的不是同一个密钥。假如Alice和Bob想在一个不安全的线路上通信，他们在用这个信息交流之前没有任何py的信息(即:他们一开始不存在有且仅有他们两个人知道的信息)，而在这条线路上通信的所有信息都会被第三方窃听者Eve所获得。问:如何不让窃听者Eve监听到Alice和Bob的对话？

当然我们必须对发送的信息进行加密，而对称加密必须两人提前获取密钥和加密方式，这些信息都是他们一开始所不知道的，因此需要在这条线路上告知密钥和加密方式，如果在这条线路上告知，那么Eve也能对加密的数据解密从而监听他们的通话内容，那么我们采取非对称加密是最保险的。我只告诉你怎么加密，解密的密钥我自己留着，由于Eve不清楚解密方式自然就无法获取信息了。

RSA加密

首先选取两个很大的质数p,q。

令n=p*q，任意选取一个很大的质数做公钥指数，那么(n,e)就形成了公钥，可以用它进行加密，假如明文为m，那么密文

1
2
3
plain

c=m^e mod n

我自己生成的p,q做运算φ(n)=(p-1)(q-1)

d=inverse(e,φ(n))，inverse函数为求模逆元函数

(n,d)就是私钥，是只有我们自己知道的。

我拿到密文c后我可以用d还原明文

1
2
3
plain

m=c^d mod n

RSA加密的破解

破解的关键在于分解n的质因数，如果分解得到的p,q那么我们就很容易推得私钥d。

在应用当中，n一般有2048位，基本是破解不出的，而在比赛的时候n就只有不到百位，用一些在线工具也是很快可以破解得到p和q的。

但是拿到了一个很大位数的私钥d那也不顶用啊，算还是算不了啊，这个时候可以用第三方解密包RSA，也可以手写算法解决，作为一个ACMer，就得把珍藏已久的快速幂算法拿出来了，由于python支持大数，所以我会用python写。

例题:[SUCTF2019]SignIn

拿到elf文件先拖进IDA打开字符串窗口(shift+F12)，发现很容易看到字符串[input flag]，那么跟进去找到函数main()

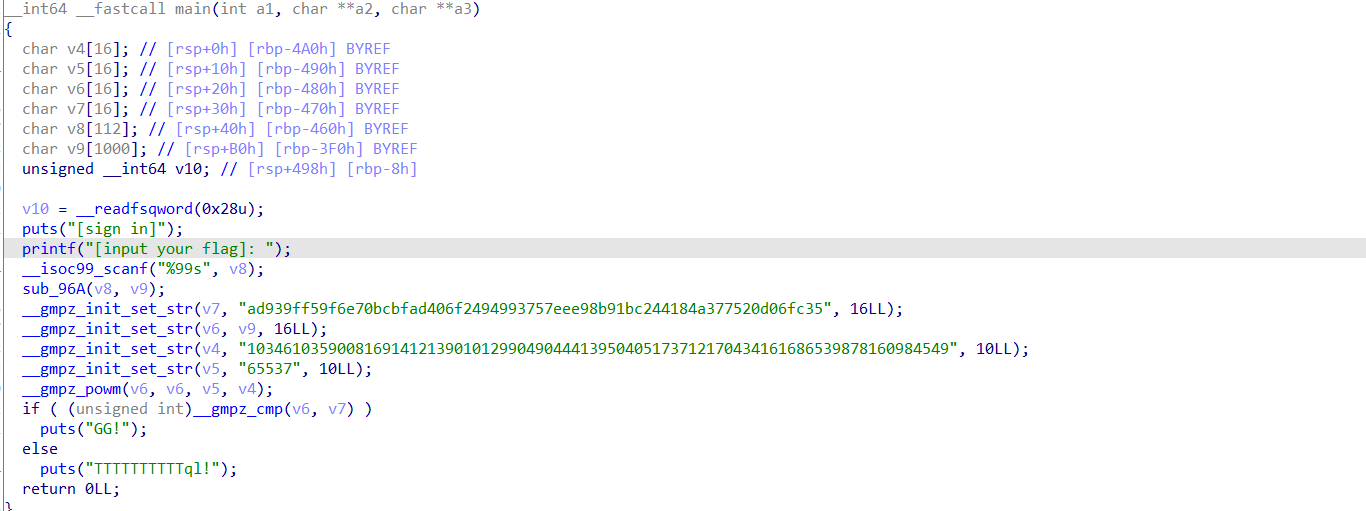
发现多了很多不认识的函数，但是根据它的参数也可以很容易发现这是个字符串赋值的函数，而且后面加了参数10或者16很像它的进制。后面的GG和TTTTTTql!肯定就是判断你输入的flag的正误了。

从头开始分析，输入的是v8字符串，v8经过了sub_96A函数的洗礼，跟进去看看逻辑关系。

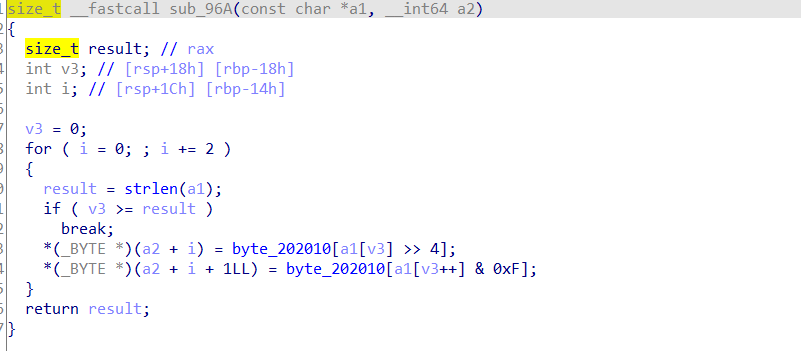
很容易发现它是把a1字符串拆解成高字节和低字节分别存储到a2[i]和a2[i+1]，至于字符串byte_202010那就是很典型的16进制表0123456789abcdef，那么我输入的它给它拆成16进制数了，那么等会逆向解回去的话这个还是很好逆回去的，那么我们ESC跳回原来的函数。

v8的值转换给了v9，v7为下面比较字符串的其中一个，然后把v9转换成16进制数赋给v6，v5=65537。其实这个特征都就已经告诉你这是RSA解密。毕竟加密指数65537是十分常见的RSA加密指数。那么下面还有一个不认识的函数，不过看它的后缀powm，pow你就很容易看出来是取次方，然后m不就是模mod了么(手动滑稽)。所以这个函数实现的功能等价于一个表达式

1
v6=v6^v5%v4

相当于v6是我们输入的，然后这个结果我们是知道的，模数n和指数e我们也知道，那么就对它结果(v7)进行RSA解密。

1.破解得到p,q，在线工具

2.编写脚本解密，这里用第三方包解密我就不演示了，主要看看解密的过程。

脚本中的数一律为10进制，转换的简单方法:把数复制到python交互窗口加上前缀0x就可以输出它的10进制数值了。

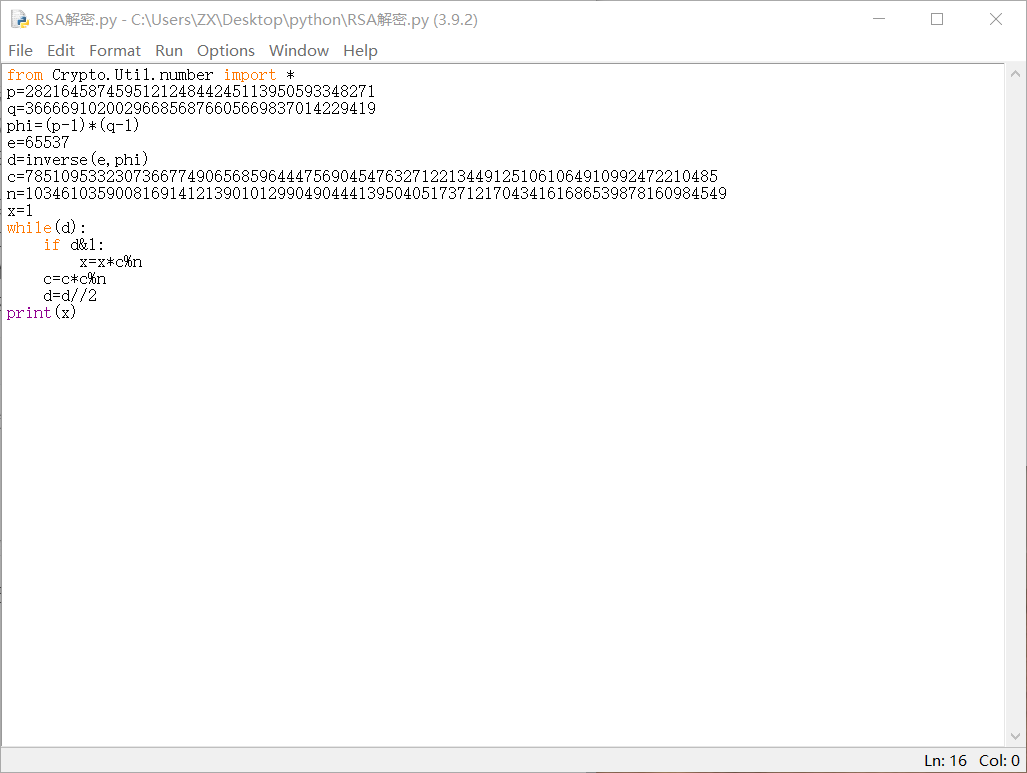
快速幂的脚本

1
2
3
4
5
6
7
8
9
python

x=1
while(d):
    if d&1:
        x=x*c%n
    c=c*c%n
    d=d//2
print(x)

得到数值185534734614696481020381637136165435809958101675798337848243069。

这里还要转回16进制再被逆回去处理，因为它以开始也就是16进制的，我们还用pythonhex(185534734614696481020381637136165435809958101675798337848243069)得到16进制数。

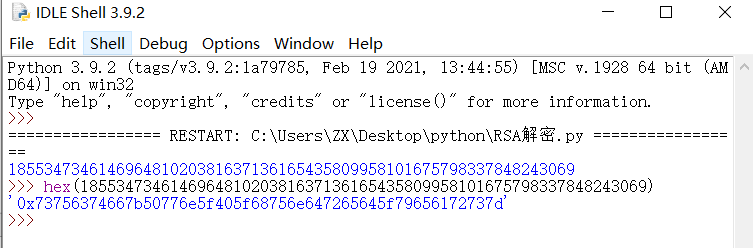
最后一步就可以写脚本做最后一步解密了，这一步很简单，就是16进制转字符串，这个我喜欢用C++写，我感觉会比较方便。

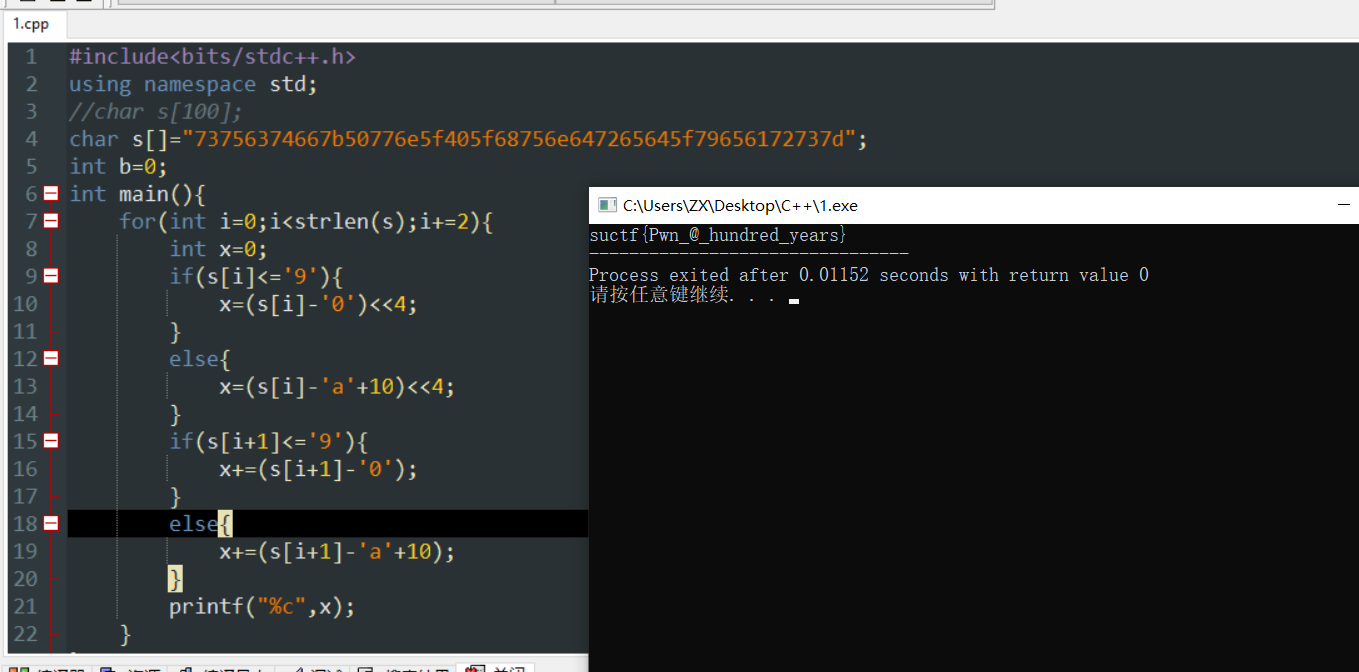
得到flag

本篇所有的exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
python

#RSA解密脚本
from Crypto.Util.number import *
p=282164587459512124844245113950593348271
q=366669102002966856876605669837014229419
phi=(p-1)*(q-1)
e=65537
d=inverse(e,phi)
c=78510953323073667749065685964447569045476327122134491251061064910992472210485
n=103461035900816914121390101299049044413950405173712170434161686539878160984549
x=1
while(d):
    if d&1:
        x=x*c%n
    c=c*c%n
    d=d//2
print(x)
c++

//hex2raw脚本
#include<bits/stdc++.h>
using namespace std;
//char s[100];
char s[]="73756374667b50776e5f405f68756e647265645f79656172737d";
int b=0;
int main(){
    for(int i=0;i<strlen(s);i+=2){
        int x=0;
        if(s[i]<='9'){
            x=(s[i]-'0')<<4;
        }
        else{
            x=(s[i]-'a'+10)<<4;
        }
        if(s[i+1]<='9'){
            x+=(s[i+1]-'0');
        }
        else{
            x+=(s[i+1]-'a'+10);
        }
        printf("%c",x);
    }
}

本作者也是没想到啊，学逆向要把加密看那么透的，当时学RSA偷懒了啊，所以导致昨天捡起又花了很多时间，不过也好，加深了我对RSA算法的印象。